不变风险最小化（IRM）

声明：笔者利用AI辅助阅读论文，因此以下内容大部分由AI生成，请谨慎看待

学习完这篇论文后，笔者推荐看一下这篇文章：https://zhuanlan.zhihu.com/p/567666715

• 论文标题：Invariant Risk Minimization
• 作者：Martin Arjovsky, Léon Bottou, Ishaan Gulrajani, David Lopez-Paz
• 发表信息：International Conference on Machine Learning (ICML), 2020
• 版本与访问：arXiv:1907.02893v3 [stat.ML]，DOI 链接：https://doi.org/10.48550/arXiv.1907.02893
• 官方资源：配套代码可参考原作者团队维护的 GitHub 仓库（如 facebookresearch/invariant-risk-minimization）

ps: 没有找到好的封面，借用知乎用户 @小张小张几点了 的文章图片：https://zhuanlan.zhihu.com/p/584303169，图片保留水印·

一、引言

文档第一部分 “引言” 是整个研究的 “问题提出与动机铺垫”—— 它先点出传统机器学习的核心痛点，再用直观例子具象化问题，接着分析问题根源，最后引出 “不变风险最小化（IRM）” 的设计思路和核心贡献。下面从核心问题、具象化例子、问题根源、IRM 动机、核心贡献五个维度，用通俗语言拆解：

1.1 核心痛点

核心痛点：传统机器学习“学错了东西”

传统机器学习（比如图像分类、推荐系统）的核心逻辑是 “最小化训练误差”—— 比如让模型在训练数据上尽可能少犯错。但第一部分开篇就指出：这种逻辑有个根本性缺陷 —— 数据本身带 “偏见”，模型会把这些偏见当成 “规律” 学进去。

具体来说，数据的 “偏见” 来自三个常见问题：

1. 选择偏差：数据采集时的 “取样不随机”。比如要收集 “猫的图片”，结果只收集了 “白天室内的家猫”，没收集 “夜晚户外的流浪猫”；
2. 混杂因素：有个隐藏变量同时影响 “输入” 和 “目标”，导致两者产生虚假关联。比如 “冰淇淋销量” 和 “溺水人数” 正相关 —— 不是因为吃冰淇淋导致溺水，而是 “高温” 这个混杂因素让两者都增加；
3. 其他数据特殊性：比如设备误差（用模糊相机拍的照片）、标注偏差（标注员把 “狼” 误标成 “狗”）。

这些偏见会让模型学到 “虚假相关性”（比如 “白天室内”=“猫”），而不是 “真实规律”（比如 “猫的轮廓、耳朵形状”=“猫”）。最终的后果是：模型在训练数据上表现好，但遇到 “和训练数据不一样的新场景” 就翻车—— 这就是 “分布外泛化失败”，也是机器学习没能实现真正人工智能的关键原因。

1.2 具象化例子

用 “奶牛骆驼分类” 例子：让 “虚假关联” 看得见

为了让抽象的 “虚假关联” 更直观，文档举了一个经典的思想实验 —— 这个例子是理解后续所有内容的 “钥匙”：

1.2.1 实验设定

任务：训练模型区分 “奶牛” 和 “骆驼” 的图片。
数据问题：由于 “选择偏差”，训练数据里

• 90% 的奶牛图片拍自 “绿色牧场”；
• 90% 的骆驼图片拍自 “沙漠”。

1.2.2 模型的 “取巧操作”

当用这个数据训练卷积神经网络后，你会发现一个诡异的现象：

• 模型在训练数据上准确率很高；
• 但给它一张 “沙滩上的奶牛” 图片，模型会错判成 “骆驼”。

1.2.3 原因拆解

原来模型根本没学 “奶牛和骆驼的形状差异”（这是真实规律），而是学了 “背景颜色” 这个 “虚假关联”：

• 看到 “绿色背景” 就判为 “奶牛”；
• 看到 “米色背景” 就判为 “骆驼”。

这个例子完美体现了传统机器学习的问题：最小化训练误差让模型 “走捷径”，把 “数据偏见” 当成了 “核心规律”。

1.3 问题根源

问题根源：传统方法 “破坏了关键信息”

为什么传统方法会学错？第一部分指出了两个核心原因，都和 “数据处理方式” 有关：

1.3.1 依赖 “训练测试同分布（iid）假设”

传统机器学习有个默认前提：训练数据和测试数据是 “从同一个场景里随机抽的”（独立同分布，简称 iid）。为了满足这个假设，人们会把所有数据 “打乱后拆分” 成训练集和测试集 —— 比如把 “牧场奶牛、沙漠骆驼” 的图片打乱，再分 80% 当训练、20% 当测试。

但现实中，测试数据往往来自 “新场景”（比如沙滩奶牛），和训练数据 “不同分布”—— 这个 iid 假设本身就是 “理想情况”，和真实世界脱节。

1.3.2 “打乱数据” 毁掉了 “区分虚假 / 真实关联的线索”

文档里有个关键观点：“打乱数据” 是我们人为做的，不是自然规律。
比如原始 NIST 手写数据集（包含不同书写者、不同书写条件的数据），为了让训练测试 “同分布”，人们把数据打乱，让训练集和测试集的 “书写者比例” 一致 —— 但这样做的代价是：

• 丢失了 “不同书写者之间，哪些特征是稳定的”（比如 “数字 8 的两个圈” 是所有书写者都会有的稳定特征）；
• 也丢失了 “数据来源 / 采集条件变化时，分布怎么变” 的信息（比如 “书写力度大的人，笔画更粗”）。

而这些 “丢失的信息” 恰恰是关键：只有知道 “环境变了，哪些特征不变”，才能区分 “虚假关联”（比如某个书写者的特殊笔画）和 “真实规律”（比如数字的核心结构）。

1.4 IRM动机

IRM 的核心思路：换个角度 ——“从多环境找不变性”

既然 “打乱数据” 不行，第一部分提出了一个反常识的思路：不打乱数据，反而要把训练数据按 “环境” 分开，专门学 “跨环境不变的关联”。

1.4.1 什么是 “环境”？

这里的 “环境” 不是 “自然环境”，而是 “数据的采集场景”—— 比如：

• 环境 1：A 国的牧场（80% 奶牛在绿草地，20% 在其他地方）；
• 环境 2：B 国的牧场（90% 奶牛在绿草地，10% 在其他地方）；
• 环境 3：沙漠边缘的农场（30% 奶牛在绿草地，70% 在沙地）。

每个环境的 “数据偏见” 不同（草地奶牛比例不同），但 “真实规律” 不变（奶牛的形状）。

1.4.2 为什么 “跨环境不变的关联” 是有用的？

文档的核心直觉是：
虚假关联会随环境变，真实关联（因果关联）会跨环境不变。
比如：

• 虚假关联（奶牛→绿草地）：环境 1 里 80%，环境 2 里 90%，环境 3 里 30%—— 随环境变；
• 真实关联（奶牛→特定形状）：不管哪个环境，奶牛的 “四条腿、两个角、流线型身体” 这些特征都不变 —— 跨环境稳定。

如果模型能学到 “跨所有训练环境都不变的关联”，那么这种关联大概率是 “因果关联”，能在没见过的新环境（比如沙滩奶牛）里泛化。

1.5 核心贡献

为什么之前的因果方法不行？IRM 的改进点

第一部分还提到：其实之前已有研究（比如 “不变因果预测”）尝试用因果工具解决泛化问题，但这些方法有明显缺陷，无法落地到机器学习（尤其是图像、文本等复杂数据）：

1. 依赖 “因果图” 假设：需要先知道 “变量之间的因果关系图”（比如 “X1→Y→X2”），但面对像素、文本等感知数据，根本画不出这样的图（你没法说 “哪个像素是哪个变量的原因”）；
2. 只适用于线性模型：之前的方法只能处理 “输入和输出是线性关系” 的问题，而现实中机器学习用的都是非线性模型（比如神经网络）；
3. 计算复杂度爆炸：变量越多，计算量呈指数增长 —— 比如处理 100 个变量，复杂度就高到无法计算。

正是因为这些缺陷，因果工具一直没能和机器学习 “无缝结合”。而 IRM 的目标就是解决这些问题：不依赖因果图、适用于非线性模型、能融入现有机器学习流程。

---

1.6 章节介绍

第一部分总结了整个研究的核心贡献 —— 提出 “不变风险最小化（IRM）” 这一新范式，并预告了后续章节的结构：

1. IRM 的核心原则：从多个训练环境中，找到一种 “数据表示”，使得 “基于这个表示的最优分类器，在所有环境中都一样”（通俗说：不管环境怎么变，模型判断 “是不是奶牛” 的核心标准不变）；
2. 后续章节安排：
   • 第 2 章：分析传统方法为什么无法分布外泛化；
   • 第 3 章：正式推导 IRM 的数学原理和算法；
   • 第 4 章：链接 IRM 与因果理论，说明 “为什么不变性能泛化”；
   • 第 5 章：用实验验证 IRM 的效果；
   • 第 6 章：用对话讨论未来研究方向。

1.7 小结

第一部分没有讲复杂的公式或算法，而是做了三件事：

1. 提痛点：传统机器学习学错东西，因为继承了数据偏见；
2. 举例子：用奶牛骆驼分类，让 “虚假关联” 和 “泛化失败” 看得见；
3. 给方向：指出问题根源是 “打乱数据丢信息”，提出 “多环境找不变性” 的思路，并说明 IRM 能弥补之前因果方法的缺陷。

二、泛化的多面性

文档第二部分 “泛化的多面性” 是整个研究的 “问题诊断环节”—— 它先明确了 “分布外泛化” 的目标，再用一个具体例子拆解 “不变关联” 和 “虚假关联” 的区别，最后逐一分析传统方法为何无法解决分布外泛化，为后续提出 IRM 铺垫。下面从核心设定、关键示例、传统方法批判三个维度，用通俗语言详细拆解

2.1 核心设定

2.1.1 环境

要理解这部分，首先得抓住 “环境” 这个关键概念 —— 它是整个分析的基础，也是区别于传统机器学习的核心。

文档里的 “环境” 不是指 “自然环境”，而是数据的 “采集场景” ：比如不同的测量设备、不同的拍摄地点、不同的时间、不同的实验条件（甚至是 “假设的极端场景”，比如 “关闭太阳”）。
举个实际例子：要训练 “识别猫” 的模型，“环境 1” 可能是 “白天室内拍的猫”，“环境 2” 是 “夜晚户外拍的猫”，“环境 3” 是 “用模糊手机拍的猫”—— 这三个就是不同的 “训练环境”，而 “所有环境”（(E_{all})）还包括 “雨天拍的猫”“幼猫” 等没见过的场景。

2.1.2 分布外泛化的目标

传统机器学习只关心 “在和训练数据相似的测试集上表现好”（比如把同一批数据打乱分训练 / 测试），但 IRM 要解决的是 “在没见过的新环境上表现好”—— 这就是 “分布外泛化（OOD 泛化）”。
文档用数学公式定义了这个目标：
(R^{OOD}(f)=\max {e \in \mathcal{E}{all }} R^{e}(f))
通俗说就是：让预测器f在 “所有可能环境”（包括没见过的）里的 “最坏表现” 尽可能好。
其中(R^e(f))是 “预测器f在环境e下的风险（平均误差）”，比如 “在‘雨天猫’环境下，模型分类错误率是多少”。

2.2 关键示例

“线性回归示例” 看懂 “不变关联” 和 “虚假关联”

文档用 “示例 1” 把抽象的 “不变性” 具象化 —— 这是理解后续内容的关键，一定要吃透。

2.2.1 示例的 “因果结构”（谁是真因，谁是假象）

先看数据是怎么生成的（结构方程模型）：

• (X_1)：从 “均值 0、方差(\sigma^2)” 的高斯分布里抽（相当于 “真实原因”，比如猫的轮廓）；
• Y：由(X_1)加 “均值 0、方差(\sigma^2)” 的噪声生成（Y是目标，比如 “是否是猫” 的标签，(X_1)是决定Y的核心）；
• (X_2)：由Y加 “均值 0、方差 1” 的噪声生成（(X_2)是 “Y的结果”，相当于 “猫的背景颜色”—— 因为Y变了(X_2)才变，不是Y的原因）。

简单说：(X_1)是Y的 “因”，(X_2)是Y的 “果” ——(X_1)和Y的关联是 “因果关联”，(X_2)和Y的关联是 “虚假关联”（因为(X_2)是跟着Y走的，不是真的决定Y）。

2.2.2 不同环境下的 “关联变化”（谁不变，谁会变）

“环境变化” 体现在哪里？文档里是 “调整(\sigma^2)的值”（比如训练环境 1：(\sigma^2=10)；训练环境 2：(\sigma^2=20)）。我们看三种回归方式的结果：

回归方式	系数(\hat{\alpha}_1)（(X_1)的权重）	系数(\hat{\alpha}_2)（(X_2)的权重）	是否 “不变”？
只看(X_1)	1（不管(\sigma^2)怎么变，都是 1）	0	✅ 不变
只看(X_2)	0	(\sigma^2/(\sigma^2+0.5))（(\sigma^2)变，值就变）	❌ 变
同时看(X_1+X_2)	(1/(\sigma^2+1))（(\sigma^2)变，值变）	(\sigma^2/(\sigma^2+1))（(\sigma^2)变，值变）	❌ 变

关键结论：

• 只有 “只看(X_1)” 的回归是 “不变” 的 —— 不管环境怎么变（(\sigma^2)怎么调），系数都不变；
• 看(X_2)的回归都是 “随环境变” 的 —— 因为(X_2)和Y的关联是 “虚假的”，环境一变，这种关联就断了。

2.2.3 为什么“不变关联” 能泛化？

文档里有个极端测试：如果让(X_2)趋近于无穷大（比如 “背景颜色” 极端夸张），会发生什么？

• 依赖(X_2)的预测器（比如只看(X_2)或看(X_1+X_2)）：误差会趋近于无穷大（因为(X_2)太大，把(X_1)的作用盖过了）；
• 只看(X_1)的预测器：误差始终有限（因为(X_1)是真因，不管(X_2)怎么变，(X_1)和Y的关系不变）。

这就是 “分布外泛化” 的本质：只有抓住 “不变的因果关联”，才能在没见过的极端环境里不翻车。

2.3 传统方法批评

四种传统方法的 “翻车现场”—— 为什么它们解决不了泛化？

文档接下来分析了四种主流方法，逐一指出它们的局限 —— 核心问题都是 “没抓住不变性”，要么被虚假关联带偏，要么找错了 “不变的对象”。

2.3.1 经验风险最小化（ERM）：最常用，但最容易 “学错”

• 思路：把所有训练环境的数据混在一起，让模型在 “合并数据” 上的误差最小（比如把(\sigma^2=10)和(\sigma^2=20)的数组合并，学一个能拟合所有数据的回归）。
• 翻车原因：合并数据后，(X_2)和Y的虚假关联依然很强（比如(\sigma^2)大时，(X_2)和Y的相关性更高），ERM 会给(X_2)分配很大的权重 —— 结果就是 “在训练环境里误差小，但换个环境（比如(\sigma^2=1000)）就失效”。
• 通俗类比：相当于学生把所有练习题混在一起背答案，没理解知识点，换个题型就不会了。

2.3.2 鲁棒学习：看似 “防极端”，实则和 ERM 没区别

• 思路：不追求 “平均误差小”，而是 “在最坏环境下的误差最小”（比如让 “(\sigma^2=10)” 和 “(\sigma^2=20)” 里的最大误差尽可能小），还会加 “环境基准值(r_e)”（比如用Y的方差当基准，避免噪声大的环境影响）。
• 翻车原因：文档用 “命题 2” 证明了一个关键结论 ——鲁棒学习本质上还是 “加权平均误差最小化”（只是给不同环境的误差加了不同权重，比如给噪声小的环境加更大权重）。 这意味着它和 ERM 一样，还是会依赖(X_2)的虚假关联 —— 比如如果两个训练环境的(\sigma^2)都大，鲁棒学习依然会给(X_2)大权重，到(\sigma^2)小的新环境就翻车。

2.3.3 领域自适应：匹配 “特征分布”，但找错了 “不变对象”

• 思路：学一个数据表示(\Phi)（比如把(X_1、X_2)转成新特征），让 “不同环境下(\Phi)的分布一致”（比如让(\sigma^2=10)和(\sigma^2=20)的(\Phi(X))分布一样），再在(\Phi)上训练分类器。
• 翻车原因：它找的 “不变” 是 “特征分布不变”，但真实的 “不变关联” 是 “(X_1)和Y的关系不变”—— 而(X_1)的分布本身是随环境变的（(\sigma^2)变了，(X_1)的方差就变了）。 比如 “猫的轮廓（(X_1)）在白天和夜晚的分布不一样（白天清晰，夜晚模糊）”，领域自适应要强行让 “轮廓的分布一致”，反而会破坏真正的不变性。

2.3.4 不变因果预测（ICP）：匹配 “残差分布”，但条件太苛刻

• 思路：找一个变量子集（比如只选(X_1)），让 “基于这个子集的回归残差（预测值和真实Y的差）在所有环境下分布一致”—— 认为这样的子集就是 “因果变量”。
• 翻车原因：它要求 “残差分布不变”，但在示例 1 里，Y的噪声方差是随环境变的（(\sigma^2)变了，Y的噪声就变了），导致残差分布也会变 ——ICP 因此无法识别出(X_1)是真因，反而可能把(X_1)排除在外。 简单说：ICP 的 “残差分布不变” 条件太严格，现实中很多场景（比如噪声变化）都满足不了。

2.4 小结

第二部分的核心结论：传统方法的 “共性问题”

这四种方法看似思路不同，但都没解决分布外泛化的核心 ——没能力区分 “不变的因果关联” 和 “随环境变的虚假关联”：

• ERM 和鲁棒学习：只关心 “拟合训练数据”，不管关联是不是因果的；
• 领域自适应：关心 “特征分布不变”，但 “分布不变” 不等于 “关联不变”；
• ICP：关心 “残差分布不变”，但条件太苛刻，无法应对噪声变化等现实情况。

正是因为传统方法都有这个缺陷，文档才要提出 IRM—— 一个专门 “找不变因果关联” 的新范式。

三、不变风险最小化的算法

文档第三部分 “不变风险最小化的算法” 是整个研究的 “技术核心”—— 它从数学定义出发，先明确 “不变性” 的严格标准，再拆解 “理想 IRM 优化问题” 的难点，最后通过一系列简化和改进，推导出可落地的实用算法（IRMv1）。这部分本质是 “把第一部分的直觉、第二部分的问题，转化为可计算的数学公式和代码逻辑”。

下面从核心定义、理想优化问题、优化难点与解决方案、实用算法（IRMv1）、实现细节与局限性五个维度，用 “直觉 + 公式 + 例子” 的方式拆解，避免陷入纯数学推导的晦涩。

3.1 核心定义

3.1.1 什么是 “能引出不变预测器的数据表示”？

要设计算法，首先得明确 “目标”—— 到底什么样的数据表示（比如提取 “动物形状” 的特征），才算 “好的、能带来不变性的表示”？文档用 “定义 3” 给出了严格答案，这是整个 IRM 算法的基石。

定义 3 的通俗解读

定义 3：若存在一个分类器w（比如 “看形状判断是否是奶牛” 的规则），使得：

• 对所有训练环境e（牧场、沙滩、沙漠），这个w都是 “基于数据表示(\Phi)的最优分类器”（即没有其他分类器能在(\Phi)上比w的误差更小）； 则称 “数据表示(\Phi)能引出跨环境的不变预测器(w \circ \Phi)”（(w \circ \Phi)就是 “用(\Phi)提特征、用w做分类” 的完整预测器）。

3.1.2 为什么定义3等价于 “不变关联”？

结合第二部分的 “条件期望” 直觉：对均方误差（回归）、交叉熵（分类）等常见损失，“最优分类器” 本质是 “条件期望(\mathbb{E}[Y|X])”（比如 “看到‘四条腿 + 两个角’的特征，预测是奶牛的概率”）。
因此，定义 3 等价于：对所有环境e和(e')，只要特征(\Phi(X^e)=h)（比如 “形状特征是 h”），就有(\mathbb{E}[Y^e|\Phi(X^e)=h] = \mathbb{E}[Y^{e'}|\Phi(X^{e'})=h])。
通俗说：相同的特征h，在任何环境下对应 “目标Y的期望” 都一样—— 这正是 “不变关联” 的本质（比如 “‘四条腿 + 两个角’的特征，不管在牧场还是沙滩，对应‘是奶牛’的概率都一样”）。

3.1.3 科学类比：让算法像科学家一样找规律

文档举了个很形象的例子：牛顿发现 “苹果落地” 和 “行星运动” 服从同一引力公式 —— 这就是 “用正确的变量（质量、距离）描述现象，规律跨场景不变”。IRM 的目标正是让模型做类似的事：找到 “能让预测规则跨环境不变的数据表示”，就像科学家找到 “能让物理定律跨场景不变的变量”。

3.2 理想的 IRM 优化问题：双层优化的 “困境”

明确目标后，文档把 “找不变表示” 转化为一个数学优化问题 —— 但这个 “理想问题” 存在致命难点，无法直接计算，这也是后续改进的出发点。

3.2.1 理想 IRM 的数学表达

我们需要同时优化两个东西：

1. 数据表示(\Phi)（比如提取 “形状” 的特征提取器）；
2. 分类器w（比如基于形状判断的规则）； 目标是：

• 最小化所有训练环境的误差和（保证预测准）；
• 满足约束：w是所有环境下 “基于(\Phi)的最优分类器”（保证不变性）。

公式写出来是这样的（双层优化）：(\begin{array}{rlrl} \min {\substack{\Phi :\mathcal{X}\to \mathcal{H} \ w: \mathcal{H} \to \mathcal{Y}}} & \sum {e\in \mathcal{E}{tr}}R^e(w\circ \Phi ) \ \text{subject to} & w\in \underset{\overline{w}:\mathcal{H}\to \mathcal{Y}}{\arg \min }R^e(\overline{w}\circ \Phi ), \forall e \in \mathcal{E}{tr}. \end{array})

3.2.2 为什么这个问题 “难”？—— 双层优化的痛点

“约束条件” 是关键：对每个环境e，都要先解一个 “内层优化”（找(\overline{w})使得(R^e(\overline{w}\circ \Phi))最小），再做 “外层优化”（调(\Phi)和w）。 举个例子：如果有 10 个训练环境，每次更新(\Phi)后，都要给 10 个环境各跑一次 “找最优(\overline{w})” 的流程 —— 计算量极大，而且内层优化的 “不稳定性”（比如局部最优）会传递到外层，导致整个优化过程难以收敛。

核心矛盾：理想的 IRM 能严格保证不变性，但计算上 “不可行”；必须做简化，在 “可计算” 和 “不变性” 之间找平衡。

3.3 优化难点与解决方案

破局：从 “理想” 到 “实用” 的三步简化，文档通过 “三步改进”，把不可行的双层优化，转化为可落地的 IRMv1 算法。每一步都在解决一个具体问题，逻辑链非常清晰。

3.3.1 第一步：把 “硬约束” 变成 “软惩罚”—— 解决 “约束难满足” 问题

硬约束（“w必须是所有环境的最优分类器”）太严格，我们换个思路：不强制满足约束，而是把 “违反约束的程度” 变成一个 “惩罚项”，加到损失里—— 违反越严重，惩罚越大，倒逼模型接近约束。

具体做法是构造新的损失函数：(L_{IRM}(\Phi ,w)=\sum {e\in \mathcal{E}{tr}}R^e(w\circ \Phi )+\lambda \cdot \mathbb{D}(w,\Phi ,e)) 其中：

• 第一项(\sum R^e(\cdot))：还是 “所有环境的误差和”（保证预测准）；
• 第二项(\lambda \cdot \mathbb{D}(\cdot))：惩罚项，(\mathbb{D}(w,\Phi,e))衡量 “分类器w离‘环境e的最优分类器’有多远”，(\lambda)是 “平衡预测准度和不变性” 的超参数（(\lambda)越大，越看重不变性）；
• 关键要求：(\mathbb{D}(\cdot))必须对(\Phi)和w可微 —— 这样才能用梯度下降优化（神经网络的核心优化方式）。

3.3.2 第二步：选对 “惩罚项(\mathbb)”—— 解决 “数值不稳定” 问题

惩罚项(\mathbb{D})的设计是关键：选得不好，优化会出大问题。文档对比了两种惩罚项，最终选了能稳定优化的(\mathbb{D}_{lin})。

1. 不好的选择：(\mathbb_)（直接算分类器距离）

思路：(\mathbb{D}{dist}(w,\Phi,e) = |w - w\Phi^e|^2)，其中(w_\Phi^e)是 “环境e下基于(\Phi)的最优分类器”（比如用线性回归的正规方程¹算出来的系数）。 问题：不连续、数值爆炸（看文档图 1 的蓝色曲线）。 举个例子（用第二部分的示例 1）：

• 当数据表示(\Phi)依赖(X_2)的权重c趋近于 0（接近理想不变表示）时，(w_\Phi^e)的(X_2)系数会趋于无穷大 —— 导致(|w - w_\Phi^e|^2)突然跳变（不连续），梯度下降没法收敛到(c=0)；
• 当c趋近于无穷大（完全依赖(X_2)）时，惩罚项反而趋近于 0—— 模型会被误导去学虚假关联。

2. 好的选择：(\mathbb_)（算 “违反正规方程的程度”）

思路：绕开 “直接求(w_\Phi^e)”（避免矩阵求逆和数值爆炸），利用 “线性分类器的最优条件”—— 对线性最小二乘，最优分类器(w_\Phi^e)满足 “正规方程”：(\mathbb{E}[\Phi(X^e)\Phi(X^e)^\top] w_\Phi^e = \mathbb{E}[\Phi(X^e)Y^e]) 因此，“w是不是最优”，等价于 “w是否满足这个方程”—— 违反方程的程度，就是惩罚项：(\mathbb{D}_{lin}(w,\Phi,e) = \left| \mathbb{E}[\Phi(X^e)\Phi(X^e)^\top] w - \mathbb{E}[\Phi(X^e)Y^e] \right|^2)

优势（看文档图 1 的绿色曲线）：

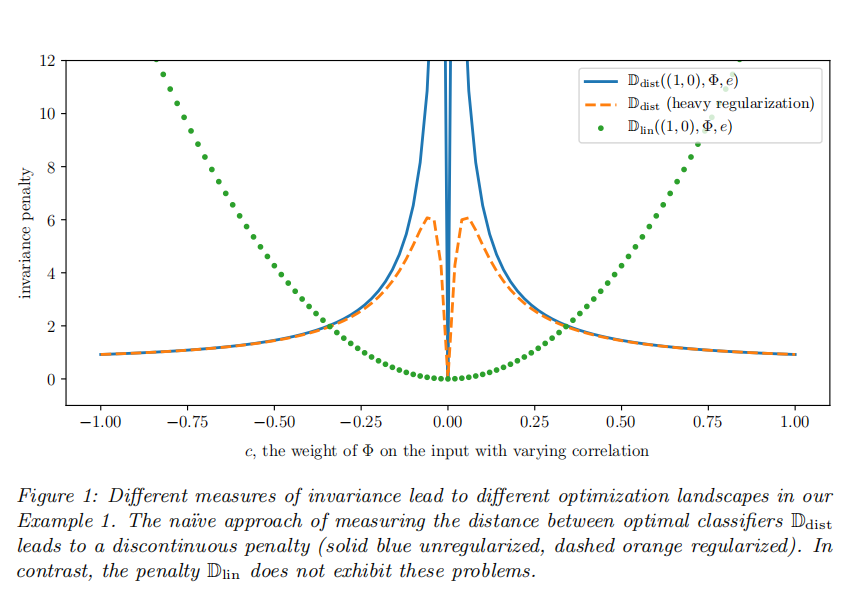
• 光滑连续：是(\Phi)和w的多项式函数，没有跳变，梯度下降能稳定优化；
• 目标明确：在 “理想不变表示”（比如(c=0)）处达到最小值 0，不会被虚假关联误导；
• 等价性：(\mathbb{D}_{lin}=0)当且仅当w是环境e的最优分类器 —— 严格对应定义 3 的约束。

3.3.3 第三步：固定分类器w—— 解决 “参数冗余” 问题

即便用了(\mathbb{D}{lin})，优化((\Phi, w))仍有一个问题：参数过度冗余。比如：对任意非零常数(\gamma)，“(\Phi' = \gamma \Phi)、(w' = w/\gamma)” 的预测结果和原来一样（(w' \circ \Phi' = w \circ \Phi)），但惩罚项(\mathbb{D}{lin})会随(\gamma)变化 —— 导致模型可以通过 “缩放(\gamma)” 让惩罚项趋近于 0，却不提升真实泛化能力²。

解决方案：固定分类器w为一个已知值，只优化数据表示(\Phi)。 文档进一步证明：固定w为标量 1.0 就足够了（不用复杂的向量），这是整个简化中最巧妙的一步。

3.3.4 为什么 “标量(w=1.0)” 就够了？（定理 4 的直觉）

定理 4 用线性代数证明了一个关键结论：任何线性不变预测器，都能分解成 “秩 1 的数据表示(\Phi)” 和 “标量分类器(w=1.0)”³。 通俗说：比如 “最优不变预测器是(Y=1 \cdot X_1 + 0 \cdot X_2)”，我们可以把它拆成：

• 数据表示(\Phi(X) = X_1)（只提取(X_1)的特征，秩 1）；
• 分类器(w=1.0)（直接用(\Phi(X))作为预测结果）； 两者的组合就是(w \cdot \Phi(X) = 1 \cdot X_1)，和原预测器完全等价。

这意味着：我们不用再优化w，只需优化(\Phi)，让 “(1.0 \cdot \Phi(X))” 成为跨环境的不变预测器 —— 参数冗余问题彻底解决。

3.4 实用算法（IRMv1）

经过以上三步简化，理想的 IRM 终于变成了可计算的 “IRMv1”，这也是实际代码中用的版本。

IRMv1 的目标函数

(\min {\Phi: \mathcal{X} \to \mathcal{Y}} \sum{e \in \mathcal{E}{tr}} R^e(\Phi)+\lambda \cdot\left| \nabla{w | w=1.0} R^e(w \cdot \Phi)\right| ^{2})

每个部分的含义：

1. (\Phi)：不再只是 “特征提取器”，而是 “完整的不变预测器”（因为(w=1.0)固定，(\Phi(X))直接输出预测结果）；
2. 第一项(\sum R^e(\Phi))：经验风险项 —— 保证(\Phi)在所有训练环境中预测准（比如 “用(\Phi)判断奶牛，在牧场和沙滩环境中误差都小”）；
3. 第二项(\lambda \cdot |\nabla_{w=1.0} R^e(w \cdot \Phi)|^2)：不变性惩罚项
   • (\nabla_{w=1.0} R^e(w \cdot \Phi))：“当(w=1.0)时，风险(R^e)对w的梯度”；
   • 对线性损失（如均方误差），这个梯度正好对应(\mathbb{D}_{lin})的核心部分（违反正规方程的程度）；
   • 对非线性损失（如交叉熵），它衡量 “(w=1.0)离‘基于(\Phi)的最优分类器’有多远”—— 梯度越小，(w=1.0)越接近最优，不变性越强；
4. (\lambda)：平衡项 ——(\lambda)太小，模型会像 ERM 一样学虚假关联；(\lambda)太大，模型会牺牲预测准度来保不变性（可能变成 “什么都不预测的零模型”）。

3.5 实现细节

理论再好，落地还要考虑 “怎么用神经网络的小批量数据估算目标函数”—— 文档给出了关键技巧：

对不变性惩罚项中的 “梯度范数平方”，用两个独立的小批量（来自同一环境e）做无偏估计：(\sum_{k=1}^{b}\left[\nabla_{w=1.0} \ell\left(w \cdot \Phi(X_k^{e,i}), Y_k^{e,i}\right) \cdot \nabla_{w=1.0} \ell\left(w \cdot \Phi(X_k^{e,j}), Y_k^{e,j}\right)\right])

为什么用两个小批量⁴？

• 单个小批量估算梯度会有偏差（因为(\mathbb{E}[a^2] \neq (\mathbb{E}[a])^2)）；
• 用两个独立小批量的梯度乘积求和，能无偏估计 “梯度范数的期望”—— 保证训练过程稳定（具体可看附录 D 的 PyTorch 代码，核心就是用两个 batch 算梯度再相乘）。

3.6 局限性和未来方向：线性​w的潜在问题

文档没有回避算法的局限性，明确指出 “假设w是线性的” 可能存在的问题：

1. 是否会漏掉非线性不变性？ 比如 “真实的不变预测器是(Y=\Phi(X)^2)”，而 IRMv1 强制(Y=1.0 \cdot \Phi(X))—— 理论上可能抓不到这种非线性关系。 但文档认为：若(\Phi)足够灵活（比如用深度神经网络），(\Phi(X))本身可以学习到 “非线性特征”（比如(\Phi(X) = X^2)），此时线性(w=1.0)仍能等价于非线性预测器⁵。
2. 零表示的陷阱 若(\Phi(X)=0)（什么特征都不提取），则对任何w，(w \cdot \Phi(X)=0)—— 此时惩罚项为 0，但预测能力为零。不过这种情况会被 “经验风险项” 剔除（因为预测误差太大）。
3. 未来研究方向
   • 如何设计 “非线性分类器w” 的不变性惩罚项？
   • 有没有 “既不被 ERM 剔除、也不被不变性项剔除” 的非不变预测器？
   • 更大的w假设类（比如神经网络）能否用更少的环境找到不变性？

3.7 小结

第三部分的核心 ——“把直觉落地”

第三部分的逻辑链非常清晰：

1. 定目标：用定义 3 明确 “好的不变表示” 是什么；
2. 提理想：写出双层优化问题，但发现计算不可行；
3. 解难题：三步简化（硬约束→软惩罚、选(\mathbb{D}_{lin})、固定(w=1.0)），解决 “计算难、数值差、参数冗余” 问题；
4. 出算法：得到 IRMv1，给出实现细节；
5. 谈局限：不回避线性w的问题，指出未来方向。

它完成了从 “第一部分的直觉” 到 “可代码实现的算法” 的跨越 —— 是整个研究 “从理论到实践” 的关键桥梁。

四、不变性、因果性与泛化

文档第四部分 “不变性、因果性与泛化” 是整个研究的 “理论根基”—— 它不再聚焦算法设计，而是回答三个核心问题：1. 为什么 IRM 学习的 “跨训练环境不变性” 能泛化到所有环境？2. 不变性和因果性到底是什么关系？3. IRM 的泛化能力有数学理论支撑吗？ 这部分把 IRM 从 “工程算法” 提升到 “因果泛化理论” 的层面，下面用 “因果基础→泛化理论→非线性与环境数量→因果即不变性” 的逻辑，结合例子拆解，避免陷入纯理论晦涩。

4.1 结构方程模型（SEM）与干预

先补因果基础：结构方程模型（SEM）与干预 —— 理解 “环境” 的本质

要理解 IRM 的泛化能力，必须先明确 “环境差异的来源”—— 文档用 “结构方程模型（SEM）” 和 “干预” 定义环境，这是连接 “不变性” 与 “因果性” 的关键。

1. 什么是结构方程模型（SEM）？—— 数据的 “因果生成规则”

SEM 是描述 “变量间因果关系” 的数学框架，比如文档示例 1 的因果关系可以写成 SEM：

(\begin{align*} X_1 &\leftarrow \mathcal{N}(0, \sigma^2) \quad \text{（X1是“因”，无父变量，由噪声生成）} \ Y &\leftarrow X_1 + \mathcal{N}(0, \sigma^2) \quad \text{（Y的“因”是X1，加噪声）} \ X_2 &\leftarrow Y + \mathcal{N}(0, 1) \quad \text{（X2的“因”是Y，加噪声）} \end{align*})

• 因果图：SEM 对应一张无环图（DAG）—— 节点是变量（X1,Y,X2），箭头从 “因” 指向 “果”（X1→Y→X2）；
• 核心特点：每个变量的取值由 “父变量（直接原因）+ 独立噪声” 决定，噪声代表 “未被观测的随机因素”。

简单说，SEM 就是 “数据生成的因果配方”—— 知道了 SEM，就能生成任何环境下的数据；而 “环境差异” 本质是 “SEM 的干预”。

2. 什么是 “干预”？—— 环境变化的数学描述

“干预” 是改变 SEM 的某一部分，生成新环境的操作，比如：

• 干预 X2：把 X2 的生成规则从 “X2←Y + 噪声” 改成 “X2←1000”（强制 X2 为常数），得到新环境 e1；
• 干预 Y 的噪声：把 Y 的噪声方差从(\sigma^2)改成(2\sigma^2)，得到新环境 e2；
• 干预 X1：把 X1 的生成规则从 “(\mathcal{N}(0, \sigma^2))” 改成 “(\mathcal{N}(5, \sigma^2))”（X1 均值偏移），得到新环境 e3。

文档用 “定义 6” 严格定义干预：干预后得到 “干预 SEM（(C^e)）”，对应的数据集服从 “干预分布（(P(X^e,Y^e))）”——每个环境本质是 “一次干预后的 SEM”，而 “所有环境（(E_{all})）” 就是 “所有有效干预的集合”。

3. 什么是 “有效干预”？—— 保证预测任务有意义

不是所有干预都能算 “有效环境”，比如把 Y 的生成规则改成 “Y←随机噪声”（与 X 无关），此时预测 Y 变得不可能。文档 “定义 7” 明确有效干预需满足 3 个条件：

1. 因果图仍无环（干预不破坏因果关系的逻辑）；
2. Y的条件期望不变：(\mathbb{E}[Y^e | Pa(Y)] = \mathbb{E}[Y | Pa(Y)])（(Pa(Y))是 Y 的父变量，比如示例 1 中 Y 的父变量是 X1—— 这保证 “Y 与父变量的因果关系不变”，是预测的基础）；
3. Y的条件方差有限：(\mathbb{V}[Y^e | Pa(Y)])在有限范围（避免噪声过大导致信号淹没）。

简单说，有效干预只能 “改变非因果变量（如 X2）或噪声”，不能 “破坏 Y 与真实原因（如 X1）的关系”—— 这是 IRM 能泛化的前提：所有环境共享 “Y 的因果生成规则”，只是表面的非因果因素不同。

4.2 IRM泛化的核心理论

RM 泛化的核心理论：从 “训练环境不变性” 到 “所有环境泛化”

IRM 的目标是 “泛化到所有环境（(E_{all})）”，但训练时只能用到 “部分训练环境（(E_{tr})）”—— 文档通过两步推导，证明 “只要训练环境足够多样，IRM 学习的不变性就能迁移到所有环境”。

1. 第一步：不变性 + 低训练误差 → 低泛化误差

假设模型在训练环境中满足两个条件：

• 条件 1：低训练误差（(\sum_{e \in E_{tr}} R^e(\Phi) \approx 0)）；
• 条件 2：跨训练环境不变（(w=1.0)在所有(E_{tr})中都是最优分类器）。

由于 “有效干预不改变 Y 与父变量的因果关系”，而 IRM 学习的 “不变性” 正是 “Y 与父变量的因果关联”（如示例 1 中的 X1→Y），因此：

• 这个因果关联在所有环境（(E_{all})）中都成立；
• 模型在训练环境中已学好这个关联且误差低，因此在所有环境中误差也会低 —— 这就是 “分布外泛化” 的直观逻辑。

数学上，这一步可通过 “泛化误差界” 证明：一旦模型学到 “跨环境不变的因果关联”，其泛化误差会被 “训练误差 + 不变性惩罚项” 的上界控制，不会随环境变化而爆炸。

2. 第二步：训练环境 “足够多样” → 不变性迁移到所有环境

关键问题：如何保证 “训练环境的不变性” 就是 “所有环境的不变性”？—— 文档用 “线性一般位置假设” 和 “定理 9” 回答，核心是 “训练环境的多样性足够，能排除所有虚假不变性”。

（1）什么是 “线性一般位置假设”？—— 训练环境的 “多样性标准”

“线性一般位置” 是数学上的 “多样性条件”，通俗说就是：训练环境不能太相似（不能存在线性依赖），每个新环境都能提供 “新的信息”，帮助排除虚假不变性。

比如示例 1 中，若训练环境只有 “(\sigma^2=10)” 这一个，模型可能误以为 “X2 与 Y 的关联（虚假）” 是不变的；但如果有 “(\sigma^2=10)” 和 “(\sigma^2=20)” 两个环境，模型会发现 “X2 的系数随(\sigma^2)变化（虚假），X1 的系数不变（真实）”—— 这就是 “多样性” 的作用。

文档 “假设 8” 用线性代数严格定义这一条件：训练环境的数量和分布需满足 “对任意非零向量 x，环境间的‘特征协方差 - 目标协方差’向量张成的空间维度足够大”—— 本质是 “环境差异能覆盖‘虚假关联的变化范围’，让模型无法通过虚假关联拟合所有训练环境”。

（2）定理 9：多样性足够 → 不变性迁移

定理 9 是第四部分的核心，通俗结论是：

若训练环境满足 “线性一般位置”，且模型在这些环境中学习到 “秩为 r 的不变表示(\Phi)”，则这个(\Phi)在所有环境中都是不变的。

• 秩 r：表示(\Phi)提取的 “不变特征的维度”（如 r=1 表示只提取 X1 这一个不变特征）；
• 核心逻辑：如果训练环境足够多样，任何 “虚假不变性”（如 X2 与 Y 的关联）都会在某个训练环境中 “暴露变化”，被 IRM 的惩罚项排除；只有 “真实因果不变性”（如 X1 与 Y 的关联）能在所有训练环境中稳定，最终被模型学到。

比如示例 1 中，只要有 2 个满足一般位置的训练环境，IRM 就能排除 X2 的虚假关联，只保留 X1 的真实关联 —— 即便在 “X2→∞” 的极端测试环境中，模型仍能正确预测。

4.3 理论局限与实践观察

非线性不变性与环境数量：理论局限与实践观察

文档坦诚地指出了理论的局限性，并结合实验给出实践启示 —— 这部分体现了研究的严谨性。

1. 非线性不变性的理论挑战

线性 IRM 有完整的泛化理论（定理 9），但非线性 IRM（如用深度神经网络做(\Phi)）面临一个关键问题：无法定义 “非线性一般位置假设”。

线性场景中，“环境多样性” 可用 “线性代数的维度” 衡量，但非线性场景中，环境差异的 “多样性” 无法用简单的数学条件描述 —— 比如 “如何衡量两个‘非线性环境’是否足够多样？”，目前没有统一答案。

文档表示：“非线性一般位置假设的形式化与证明” 是未来研究方向，当前非线性 IRM 的泛化能力主要靠实验验证（如彩色 MNIST 实验），而非理论保证。

2. 实践启示：环境数量不需要太多

定理 9 从理论上要求 “训练环境数量随特征维度线性增长”（比如 d 维特征需要 d 个环境），但实验发现：多数场景下，2 个训练环境就足够学习到不变性。

原因是：很多现实问题中，“虚假关联的变化速度远快于真实不变性”—— 比如 “奶牛分类” 中，“背景颜色”（虚假）在 2 个环境中就会变化（牧场→沙滩），而 “奶牛形状”（真实）在所有环境中稳定。此时，2 个环境足以让 IRM 区分 “虚假” 与 “真实”。

文档推测：这类问题的特点是 “若(\mathbb{E}[Y^e | \Phi(X^e)])在 2 个环境中一致，则(\Phi)必然提取了因果不变性”—— 未来研究需明确 “哪些问题只需少量环境”。

4.4 因果和不变性

因果即不变性：重新理解因果关系

文档第四部分的升华：不变性是因果关系的核心特征—— 这一观点打破了 “因果必须用因果图描述” 的传统认知，为机器学习与因果结合提供了新视角。

1. 传统因果方法的局限：依赖因果图

传统因果方法（如佩尔的 do - 演算、鲁宾的潜在结果模型）需要先知道 “因果图”（变量间的因果关系），但在机器学习的复杂场景中（如图像、文本），因果图根本无法绘制 —— 比如 “无法说清‘哪个像素是猫的原因’”。

2. 不变性：因果关系的 “可观测代理”

文档提出：因果关系的本质是 “干预下的不变性”—— 不需要因果图，只要一个关联在 “所有有效干预（环境）” 中稳定，它就是因果关联。

比如：

• 理想气体定律(PV=nRT)：无法用因果图描述 “P、V、T 谁是因谁是果”，但它在 “温度变化、体积变化” 等所有有效干预中稳定 —— 因此是因果规律；
• 图像分类：“猫的形状特征与标签的关联” 在 “背景变化、光照变化” 等环境中稳定 —— 因此是因果关联，即便我们画不出 “像素→形状→标签” 的详细因果图。

对机器学习而言，这一观点的价值在于：无需先构建因果图，只需通过多环境数据学习 “不变关联”，就能间接捕捉因果关系——IRM 正是基于这一思想，让模型在 “无因果图先验” 的情况下，通过数据自动发现因果不变性。

4.5 IRM泛化本质

第四部分的核心结论：IRM 泛化的本质是 “因果不变性”

第四部分用因果理论为 IRM “正名”，核心结论可总结为 3 点：

1. 环境的本质是干预：所有环境都是 “对同一 SEM 的有效干预”，共享 “Y 的因果生成规则”—— 这是 IRM 能泛化的前提；
2. IRM 泛化的逻辑链：多样的训练环境→排除虚假关联→学到因果不变性→在所有环境中泛化；
3. 因果即不变性：无需因果图，不变性是因果关系的 “可观测特征”——IRM 为 “机器学习自动发现因果关系” 提供了可行路径。

简单说，第四部分告诉我们：IRM 不是 “另一种正则化方法”，而是 “基于因果理论的泛化范式”—— 它的泛化能力不是偶然的，而是源于对 “因果不变性” 的捕捉。

ps：不变的相关性不一定是因果关系，但因果一定是不变的相关性（比如月亮出来与天黑存在相关性，但月亮出来并不是天黑的原因。而地球自转才是天黑的原因，地球自转，天会黑这存相关性）

4.6 小结

第四部分的作用 —— 为 IRM “立理论根基”

如果说第三部分是 “IRM 的工程实现”，第四部分就是 “IRM 的理论灵魂”：

• 它用 SEM 和干预定义 “环境”，明确了 “泛化的场景边界”；
• 它用定理 9 证明 “线性 IRM 的泛化能力”，让算法有理论支撑；
• 它提出 “因果即不变性”，为非线性 IRM 和未来研究指明方向；
• 它坦诚理论局限，结合实验给出实践启示，体现严谨性。

理解第四部分，就能理解 “为什么 IRM 比 ERM、领域自适应等方法更能泛化”—— 因为 IRM 学的是 “因果规律”，而其他方法学的是 “数据关联”；因果规律跨环境稳定，而数据关联会随环境变化。

五、实验

文档第五部分 “实验” 是整个研究的 “实证支撑”—— 通过合成数据实验（控制变量，验证理论）和彩色 MNIST 实验（贴近真实图像任务，验证非线性场景），直接对比 IRM 与传统方法（ERM、ICP）的性能，证明 “IRM 能有效学习不变性，实现分布外泛化”。下面按 “实验设计逻辑→结果解读→核心结论” 的顺序，拆解两个实验的细节，重点讲清 “实验要验证什么”“为什么这么设计”“结果如何支持 IRM 的优势”。

5.1 合成数据实验

第一个实验：合成数据实验 —— 控制变量，验证因果特征提取能力

合成数据实验的核心目标是：在 “已知因果结构” 的理想场景中，验证 IRM 能否准确识别 “因果特征”（如示例 1 中的 X₁）、剔除 “虚假特征”（如 X₂），同时对比 ERM（经验风险最小化）和 ICP（不变因果预测，此前的最优方法）的不足。

1. 实验设计：扩展示例 1，模拟更真实的复杂场景

为了全面测试 IRM 的鲁棒性，实验在示例 1 的基础上做了 3 点关键扩展（对应文档中的图 3），模拟现实中常见的 “模型误设”“特征混合”“混杂变量” 等问题：

扩展方向	具体设计	目的
1. 维度提升	将 X₁、X₂的维度从 1 维均提升到 10 维	模拟高维特征场景（如图像的像素），测试 IRM 在高维中筛选因果特征的能力
2. 加入隐藏混杂变量 H	新增 10 维隐藏变量 H，H 会同时影响 X₁、Y、X₂（如 H 是 “光照强度”，同时影响 “物体形状（X₁）”“标签判断（Y）”“背景颜色（X₂）”）	模拟 “未观测混杂”（现实数据中常见），测试 IRM 抗混杂的能力
3. 特征混合（S≠I）	部分场景中，不直接观测真实特征 Z₁（因果）、Z₂（虚假），只观测混合后的 X=S (Z)（S 是正交矩阵，如 “像素被随机打乱”）	模拟 “特征不可直接观测” 的场景，测试 IRM 能否从混合特征中恢复因果结构

此外，实验还设计了 8 种具体场景（用首字母组合标识），覆盖 “有无混杂”“同 / 异方差噪声”“特征是否混合” 等情况，确保结果的全面性：

• 全观测（F）/ 部分观测（P）：F 表示无混杂（H 的影响为 0），P 表示有混杂（H 影响 X₁、Y、X₂）；
• 同方差（O）/ 异方差（E）：O 表示 Y 的噪声方差随环境变化，E 表示 X₂的噪声方差随环境变化；
• 混合观测（S）/ 非混合观测（U）：S 表示观测混合后的 X=S (Z)，U 表示直接观测 Z（S=I）。

实验数据生成逻辑（SEM）：(\begin{align*} H^e &\leftarrow \mathcal{N}(0, e^2) \quad \text{（隐藏混杂变量，方差随环境e变化）} \ Z_1^e &\leftarrow \mathcal{N}(0, e^2) + W_{h→1}H^e \quad \text{（因果特征Z₁，受H影响）} \ Y^e &\leftarrow Z_1^e \cdot W_{1→y} + \mathcal{N}(0, \sigma_y^2) + W_{h→y}H^e \quad \text{（目标Y，受Z₁和H影响）} \ Z_2^e &\leftarrow W_{y→2}Y^e + \mathcal{N}(0, \sigma_2^2) + W_{h→2}H^e \quad \text{（虚假特征Z₂，受Y和H影响）} \ X^e &= S(Z_1^e, Z_2^e) \quad \text{（观测特征X，可能是Z的混合）} \end{align*})

• 训练环境：E_tr = {0.2, 2, 5}（3 个环境，e 控制 H 和 Z₁的方差）；
• 对比方法：ERM（合并所有环境数据）、ICP（传统不变因果预测）、IRM（IRMv1，用 e=5 交叉验证正则化参数 λ）。

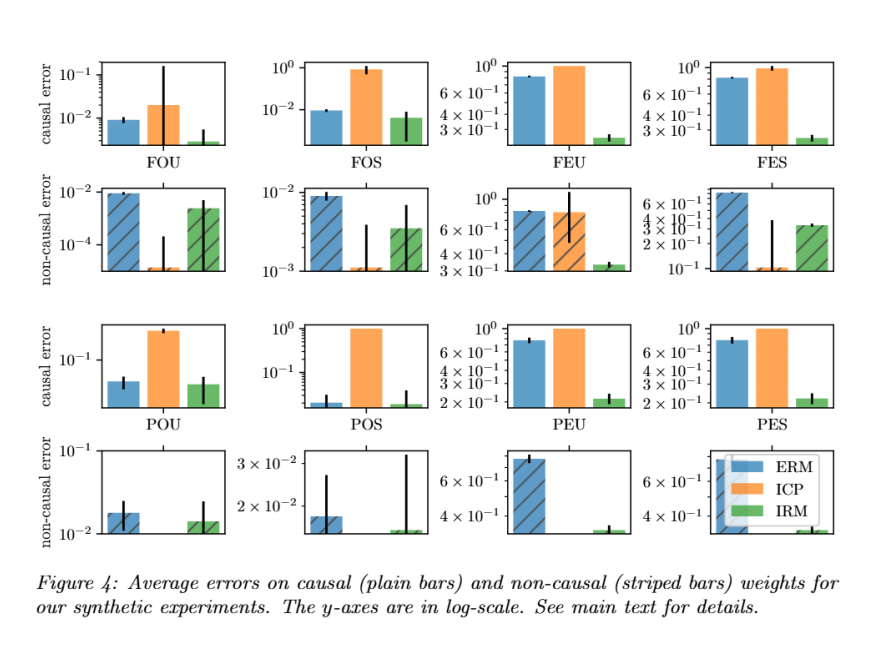
2. 评价指标：聚焦 “因果特征提取准确性”

实验用两个核心指标衡量模型性能（对应文档中的图 4），避免 “只看预测误差” 的片面性 —— 因为有些方法（如 ICP）可能预测误差低，但没学到真正的因果特征：

指标名称	计算方式	含义（目标）
因果权重误差（实心柱）	估计的因果权重(\hat{M}{1→y})与真实权重(W{1→y})的平均平方误差	衡量模型 “提取因果特征（Z₁）” 的准确性→越小越好
非因果权重误差（条纹柱）	估计的非因果权重(\hat{M}_{y→2})的范数	衡量模型 “是否剔除虚假特征（Z₂）”→理想值为 0

注：(\hat{M})是 “解混合后的权重”—— 因为部分场景中 X 是 Z 的混合（X=S (Z)），需要通过(S^\top)反推回 Z 空间的权重，确保指标能直接对应因果 / 非因果特征。

3. 实验结果：IRM 全面优于 ERM 和 ICP

图 4 的结果（纵轴为对数尺度，差异更明显）可总结为 3 个关键结论：

1. IRM 的因果权重误差最小：在所有 8 种场景中，IRM 对 “因果特征 Z₁权重” 的估计最接近真实值 —— 比如在 “FOS（全观测 + 同方差 + 混合）” 场景中，IRM 的因果误差比 ERM 小 1-2 个数量级（对数尺度下差距显著）；
2. IRM 的非因果权重误差最接近 0：IRM 能有效剔除虚假特征 Z₂，非因果权重的范数远小于 ERM（ERM 几乎完全依赖 Z₂的虚假关联）；
3. ICP 表现保守，泛化能力有限：ICP 虽能部分剔除虚假特征（非因果误差小），但会 “过度排除因果特征”（因果误差大）—— 因为 ICP 对 “残差分布不变” 的要求过严（如 Y 的噪声变化会导致残差分布变化），导致它误将 Z₁排除在因果特征之外。

核心启示：在 “已知因果结构” 的场景中，IRM 能精准定位因果特征、剔除虚假关联，且鲁棒性强（不受混杂、特征混合、噪声变化的影响），而 ERM 和 ICP 分别因 “依赖虚假关联” 和 “条件过严” 无法达到理想效果。

5.2 彩色MNIST实验

第二个实验：彩色 MNIST 实验 —— 验证非线性、复杂感知任务的泛化能力

合成数据实验验证了 IRM 在 “线性、已知因果” 场景的有效性，而彩色 MNIST 实验的目标是：在 “非线性、感知输入（图像）、虚假关联更强” 的真实场景中，验证 IRM 能否学习非线性不变性，实现分布外泛化。

1. 实验设计：构造 “颜色 - 标签” 虚假关联，逼模型做选择

实验基于 MNIST 手写数字数据集（原始为灰度图），通过 “染色” 构造强虚假关联，模拟现实中 “模型易被表面特征误导” 的场景（如奶牛分类中 “背景颜色” 比 “动物形状” 易学习）：

（1）核心矛盾设计：虚假关联强于真实关联

• 真实关联：数字本身（如 0-4 为类 0，5-9 为类 1）→ 模型需要学习 “数字形状” 这一不变特征；
• 虚假关联：颜色（红 / 绿）与标签的强相关性→ 构造上，“颜色 - 标签” 的相关性（如 80% 红色对应类 0）远强于 “数字 - 标签” 的相关性（如 60% 数字 0 对应类 0），迫使 ERM 优先学习颜色。

（2）环境构造：3 个环境，测试 “虚假关联反转” 的泛化

实验生成 2 个训练环境、1 个测试环境，关键差异是 “颜色 - 标签” 的相关性强度（用概率 p^e 控制），具体步骤：

1. 分配初步标签(\bar{y})：数字 0-4→(\bar{y}=0)，5-9→(\bar{y}=1)；
2. 翻转初步标签：以 0.25 概率翻转(\bar{y})，得到最终标签 y（增加任务难度，避免数字与标签完全对应）；
3. 采样颜色标识 z：以概率 ​p^e 翻转 y，得到 z（z=1→红色，z=0→绿色）——​p^e 是环境的核心差异：
   • 训练环境 1（e1）： ​p^e =0.2（20% 概率翻转 y→80% 红色对应原 y）；
   • 训练环境 2（e2）： ​p^e =0.1（10% 概率翻转 y→90% 红色对应原 y）；
   • 测试环境（e_test）： ​p^e =0.9（90% 概率翻转 y→10% 红色对应原 y，即 “颜色 - 标签” 相关性反转）。

（3）对比方法：4 种方法，突出 IRM 的优势

方法	核心逻辑	作用（对照）
ERM	合并两个训练环境数据，最小化交叉熵损失	baseline，验证 “依赖虚假关联” 的泛化失败
IRM	用 IRMv1 训练，最小化 “经验风险 + 不变性惩罚”	核心方法，验证能否剔除颜色、学习数字形状
随机猜测	50% 准确率	衡量模型是否优于随机
Oracle（灰度 MNIST 模型）	仅用灰度图训练（强制忽略颜色）	最优上限，验证 IRM 是否接近理想不变性

2. 实验结果：IRM 突破虚假关联，实现有效泛化

（1）准确率对比（表 1）：IRM 在测试环境中碾压 ERM

方法	训练环境准确率	测试环境准确率	关键结论
ERM	87.4±0.2	17.1±0.6	训练时依赖颜色（虚假关联），测试时因颜色反转崩溃，准确率远低于随机
IRM	70.8±0.9	66.9±2.5	训练准确率略低（未依赖颜色），但测试准确率显著提升，接近最优
随机猜测	50	50	基准线，IRM 远超随机
Oracle（灰度）	73.5±0.2	73.0±0.4	最优上限，IRM 性能接近 Oracle，证明其学到了数字形状这一不变特征

关键解读：ERM 的高训练准确率是 “虚假的”（靠颜色），而 IRM 牺牲了部分训练准确率，换来了真正的泛化能力 —— 这正是 IRM 的核心价值：不追求 “训练集上的表面误差小”，而追求 “跨环境的不变性”。

（2）模型行为分析（图 5）：IRM 的预测更接近不变性

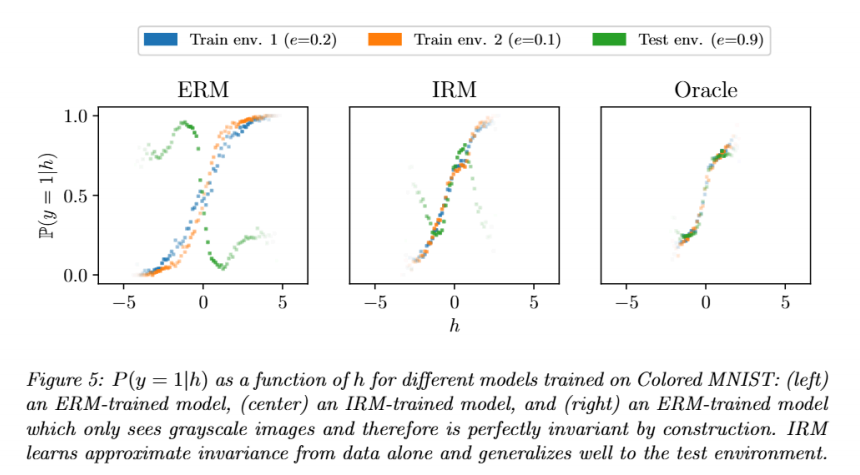
实验通过 “P (y=1|h) 曲线”（h 是模型输出的 logit 值，即 Φ(X)），直观展示不同模型的不变性：

• 横轴 h：模型对 “数字形状” 的判断（h 越大，模型认为是类 1 的概率越高）；
• 纵轴 P (y=1|h)：在给定 h 的情况下，真实标签为 1 的概率（理想情况下，不同环境的曲线应重合，即不变性）。

结果对比：

• ERM：不同环境的曲线差异极大（尤其是测试环境曲线与训练环境几乎反转）→ 证明 ERM 完全依赖颜色，h 无法反映真实数字形状；
• IRM：不同环境的曲线更接近（尤其是训练环境 1 和 2 几乎重合，测试环境曲线虽有偏差但未反转）→ 证明 IRM 学到的 h（数字形状）具有不变性，P (y|h) 跨环境稳定；
• Oracle：所有环境的曲线几乎完全重合→ 理想不变性的参照，IRM 的曲线趋势与 Oracle 一致，进一步证明 IRM 学到了数字形状。

3. 补充讨论：IRM vs 条件领域自适应

文档特别提到：条件领域自适应（C-ADA，匹配 P (Φ(X)|Y)）在该实验中可能表现与 IRM 相近，但这是 “特殊场景下的巧合”—— 因为该实验中 “数字形状的分布” 和 “P (Y|e)” 在环境间一致。若场景变化（如训练环境 1 是数字 0-4，训练环境 2 是数字 5-9，即数字分布变化），C-ADA 会因 “强制匹配 P (Φ(X)|Y)” 而失败，而 IRM 仍能通过 “P (Y|Φ(X)) 不变” 实现泛化 —— 这再次证明 IRM 对 “不变性本质” 的把握更准确。

5.3 小结

第五部分的核心结论：IRM 的有效性与通用性

两个实验从 “理想控制场景” 到 “真实感知场景”，层层递进验证了 IRM 的价值：

1. 有效性：IRM 能准确提取因果特征（合成数据）、剔除虚假关联（彩色 MNIST），泛化能力远超 ERM 和 ICP；
2. 通用性：无论是线性高维数据、带混杂变量的数据，还是非线性图像数据，IRM 都能稳定工作；
3. 合理性：IRM 牺牲部分训练准确率以换取不变性，最终在分布外场景中获得远超传统方法的性能 —— 这正是 “分布外泛化” 的核心诉求：不追求训练集上的 “完美拟合”，而追求对未知场景的 “鲁棒适应”。

简言之，第五部分用扎实的实验证明：IRM 不是理论上的 “空中楼阁”，而是能在实际任务中解决 “传统方法泛化失败” 的有效范式。

六、展望：结语对话

文档第六部分以 “苏格拉底式对话” 的形式，通过两名研究生（Eric 和 Irma）的讨论，从 “ERM 的缺陷根源”“IRM 的核心价值”“不变性的潜在应用” 三个维度，通俗拆解了 IRM 与传统机器学习的本质差异，并启发未来研究方向。对话没有复杂公式，而是用 “问题 - 讨论 - 反思” 的逻辑，把前文的理论和算法落地到 “为什么 IRM 有用”“什么时候用 IRM”“IRM 还能做什么” 等实际问题上。下面按对话的核心议题，逐模块解析：

6.1 ERM的错误前提

核心议题 1：ERM 的 “大谎言”——iid(独立同分布) 假设的破裂

对话开篇就直击 ERM 的根本缺陷：依赖 “训练数据与测试数据独立同分布（iid）” 的假设，但这一假设在现实中几乎不成立（被 Ghahramani 教授称为 “机器学习的大谎言”）。两人进一步拆解了 “非 iid 场景” 的两种核心情况，以及 IRM 的应对思路：

1. 情况 1：输入边际分布变化（协变量偏移）——P (X) 变，P (Y|X) 不变

• 场景举例：训练数据是 “白天拍的猫（X1）”，测试数据是 “夜晚拍的猫（X2）”—— 猫的特征（X）分布变了（白天清晰 / 夜晚模糊），但 “猫的特征→标签（Y）” 的关联（P (Y|X)）不变（不管白天夜晚，“四条腿 + 尖耳朵” 都是猫）。

• ERM 的问题：若训练测试 X 的支撑集（取值范围）不重叠（比如训练只有白天图，测试只有夜晚图），ERM 无法泛化 —— 因为它没学到 “跨 X 分布的不变关联”，只拟合了白天 X 的特征。

• IRM 的应对思路：

  思路 1：学习 “不变表示 Φ(X)”，让 Φ(X1) 和 Φ(X2) 的支撑集一致（比如把 “白天 / 夜晚的猫” 都转化为 “轮廓特征”），再在 Φ 上训练不变分类器。但附录 D 证明这种 “匹配特征分布” 的思路有缺陷（可能破坏因果关联）⁶。

  思路 2：假设 “不变分类器 w 的结构简单”（如线性），即便 X 的支撑集不重叠，也能通过多环境数据估计 w（比如从 “白天猫” 学 “轮廓→猫” 的线性规则，直接用到 “夜晚猫” 的轮廓上）。IRM 采用的正是思路 2，通过 “固定 w=1.0 + 优化 Φ”，避开 “匹配特征分布” 的陷阱。

2. 情况 2：条件分布变化（P (Y|X) 变）—— 反因果任务的难题

• 关键区分：Schölkopf 教授提出 “因果任务” 与 “反因果任务” 的差异：
  • 因果任务：X 是 Y 的 “因”（如 “猫的特征（X）→是否是猫（Y）”），P (Y|X) 跨环境稳定，ERM 有效；
  • 反因果任务：X 是 Y 的 “果”（如 “MNIST 像素（X）是‘数字概念（Y）’的果”），P (Y|X) 可能随环境变（比如不同书写者的像素分布不同），ERM 易失效。
• 对话的补充观点：Eric 认为 “监督学习中预测人类标注的任务是因果的”—— 因为标注过程是 “人类看到 X→产生 Y”，P (Y|X) 因标注规范而稳定（比如不同环境下，“猫的像素” 都对应 “猫” 的标签），这解释了 “为什么 ERM 在多数监督任务中有效”；但无监督 / 自监督任务（如从像素反推因果因子）是反因果的，P (Y|X) 可能变，需要 IRM 的不变性来泛化。

6.2 过参数化的陷阱

核心议题 2：过参数化的陷阱 ——ERM 为何偏爱虚假关联

对话接着讨论了神经网络 “过参数化”（参数数≥样本数）时，ERM 的另一个缺陷：优先选择 “低容量解”，导致吸收虚假关联。这正是前文 “奶牛分类”“X1 是因、X2 是果” 例子的深化：

1. 过参数化的本质矛盾

• 数学例子：假设用 X=(X1,X2) 预测 Y，其中 X1 是因（Y=1e6・X1・α1），X2 是果（X2=1e6・Y・α2・e），且输入维度 2n（n 为样本数，过参数化）。
• SGD 的偏向：过参数化时，SGD 会选 “容量最小的零误差解”⁷——X2 与 Y 的关联更直接（X2 是 Y 的线性函数），容量需求低，因此 SGD 优先学 X2 的虚假关联；而 X1 是 Y 的因，关联更复杂（需更大容量），被 SGD 忽略。
• IRM 的解决方案：通过 “不变性惩罚项”，迫使模型意识到 “X2 的关联随环境 e 变化（虚假），X1 的关联不变（因果）”，即便过参数化，也会优先学 X1—— 相当于 “用不变性打破‘低容量解 = 好解’的偏见”。

2. 容量不足的补救：IRM 与 ERM 的平衡

对话还提到 “假设类容量不足” 的场景（如用线性模型预测二次函数 Y=X²）：此时强行追求不变性，只能得到 “零预测器”（线性模型无法拟合二次关联）。

• 应对策略：通过交叉验证降低 IRM 的不变性惩罚项 λ，让模型 “适度妥协”—— 优先保证基础预测能力（ERM 的优势），再逐步提升不变性。
• 核心启示：IRM 不是 “替代 ERM”，而是 “补充 ERM”—— 在 ERM 失效的场景（分布变化、过参数化），IRM 的不变性惩罚发挥作用；在 ERM 有效的场景（容量不足、P (Y|X) 稳定），IRM 可灵活调整，避免 “为了不变性牺牲预测能力”。

6.3 IRM 的未来方向

IRM 的未来方向 —— 不变性的扩展性

对话最后跳出 “分类任务”，探讨了 IRM 在其他领域的潜力，这些方向也是前文理论的自然延伸：

1. 强化学习（RL）：episodes 作为 “环境”

• 思路：把强化学习的 “每个回合（episode）” 视为不同环境（如 “迷宫 1”“迷宫 2”“迷宫 3”），每个环境的 “状态分布” 不同，但 “动作→奖励” 的因果关联不变（如 “向右走→到达终点” 在所有迷宫中都成立）。
• IRM 的价值：学习 “跨 episodes 的不变政策”，避免 RL agent 因 “环境细节变化”（如迷宫墙壁颜色变）而失效，实现鲁棒的强化学习。

2. 公平性：群体作为 “环境”

• 思路：把 “不同人群” 视为不同环境（如 “男性群体”“女性群体”“老年群体”），公平性的核心是 “对具有相似相关特征的个体，处理方式跨群体不变”（如 “相同学历 + 相同工作经验” 的人，无论性别，都应得到相同的薪资预测）。
• IRM 的价值：通过 “群体间的不变性惩罚”，迫使模型忽略 “性别、种族” 等无关特征，只依赖 “学历、经验” 等因果特征，从机制上解决算法偏见。

3. 理论深化：群论视角的形式化

• 思路：用 “群论” 中的 “不变性”“等变性” 概念，为 IRM 提供更严谨的数学基础 —— 比如 “平移不变性”（卷积的核心）是群论中的 “群作用下的不变性”，IRM 的 “跨环境不变性” 可视为 “环境群作用下的不变性”。
• 意义：目前 IRM 的非线性理论仍不完善（如非线性一般位置假设），群论可能为 “非线性能不变性” 的惩罚项设计、泛化保证提供新工具。

6.4 小结

对话的核心价值：不是 “给答案”，而是 “启思考”

与前文的 “理论推导”“实验验证” 不同，第六部分的对话更像是 “研究总结与展望”，它的意义在于：

1. 通俗化理论：用 “奶牛、MNIST、冰淇淋与溺水人数” 等例子，把 “因果不变性”“过参数化” 等抽象概念转化为可感知的问题；
2. 澄清误解：明确 “IRM 不是 ERM 的敌人，而是补充”——ERM 在 “iid、监督、可实现场景” 中仍有效，IRM 在 “分布变化、反因果、过参数化场景” 中发挥作用；
3. 打开视野：指出 IRM 的潜力不止于 “分类任务”，而是能延伸到强化学习、公平性、群论理论等领域，为后续研究提供方向。

简言之，这段对话是整篇论文的 “灵魂升华”—— 它从 “技术细节” 回到 “问题本质”，让读者明白：IRM 的核心不是 “一个新算法”，而是 “一种新的学习哲学”——从 “拟合数据关联” 转向 “寻找因果不变性”，这正是机器学习突破 “分布外泛化” 瓶颈的关键。

---

附录

该论文附录（A-D）是对正文核心理论、算法与实验的关键补充，分别从理论扩展、数学证明、竞品缺陷分析、工程实现四个维度，解决正文未深入的技术细节与逻辑漏洞，为 IRM 的严谨性和可复现性提供支撑。以下按附录模块逐一拆解：

附录 A：额外定理 —— 线性一般位置的普遍性

附录 A 仅含定理 10，核心作用是为正文第 4 章 “IRM 泛化理论” 中的 “线性一般位置假设” 提供理论保障，证明该假设在现实场景中 “几乎必然成立”，消除 “假设过于严格、难以满足” 的担忧。

定理 10 的核心内容

设两个关键统计量：

• (\sum_{X,X}^e = \mathbb{E}[X^e (X^e)^\top])：环境e下输入特征(X^e)的协方差矩阵（对称正半定矩阵，记为(\mathbb{S}_+^{d×d})空间）；
• (\sum_{X,\epsilon}^e = \mathbb{E}[X^e \epsilon^e])：环境e下输入(X^e)与噪声(\epsilon^e)的协方差向量（(\mathbb{R}^d)空间）。

定理结论：对任意给定的({ \sum_{X,\epsilon}^e }{e \in \mathcal{E}{tr}})（噪声协方差向量集合），不满足 “线性一般位置” 的协方差矩阵集合({ \sum_{X,X}^e }{e \in \mathcal{E}{tr}})，在所有可能的协方差矩阵空间中 “测度为零”。

通俗解读

“测度为零” 意味着：在现实中随机生成多个训练环境的协方差矩阵，几乎不可能出现 “不满足线性一般位置” 的情况 —— 换句话说，“线性一般位置假设” 不是苛刻的限制，而是大多数真实场景的自然属性。这为正文定理 9（IRM 泛化能力）的实用性提供了关键支撑：无需担心训练环境 “不够多样”，只要数据来自真实场景，环境多样性通常能满足要求。

附录 B：数学证明 —— 核心命题与定理的严谨推导

附录 B 是论文的 “逻辑基石”，通过拉格朗日乘数法、线性代数、流形理论等工具，为正文 3 个核心结论提供严格数学证明，确保理论无漏洞。

B.1 命题 2 的证明：鲁棒学习等价于加权 ERM

命题 2 回顾

鲁棒学习的目标（最小化跨环境最大误差：(\min_f \max_{e \in \mathcal{E}{tr}} R^e(f) - r_e)，(r_e)为环境基线），在 KKT 可微性条件下，等价于 “最小化环境风险的加权平均”：(\exists \lambda_e \geq 0)，使得鲁棒学习的最优解是(\sum{e} \lambda_e R^e(f))的一阶驻点。

证明核心逻辑

1. 转化为约束优化：将鲁棒学习的 “max-min 目标” 转化为带约束的最小化问题 —— 最小化M， subject to (R^e(f) - r_e \leq M)（对所有e）；
2. 构造拉格朗日函数：(L(f,M,\lambda) = M + \sum_{e} \lambda_e (R^e(f) - r_e - M))，其中(\lambda_e \geq 0)是拉格朗日乘数；
3. KKT 条件推导：最优解需满足 “梯度为零”，即(\nabla_f L = \sum_{e} \lambda_e \nabla_f R^e(f) = 0)—— 这恰好是 “加权 ERM 的一阶最优条件”。

证明意义

戳破 “鲁棒学习优于 ERM” 的误区：鲁棒学习本质是 “给不同环境风险加权重”，仍属于 ERM 的扩展，无法像 IRM 那样学习跨环境不变性，最终会因依赖虚假关联导致泛化失败（如正文示例 1 中，鲁棒学习仍会给(X_2)大权重）。

B.2 定理 4 的证明：标量分类器(w=1.0)的等价性

定理 4 回顾

任何线性不变预测器(v = \Phi^\top w)（(\Phi)为数据表示矩阵，w为分类器权重），都可分解为 “秩 1 的(\Phi)” 与 “标量(w=1.0)”—— 即无需优化w，只需优化(\Phi)，让(\Phi^\top \cdot 1.0)成为不变预测器。

证明核心逻辑

1. 子空间等价性：(\Phi)的可达空间(G_\Phi = { \Phi^\top w | w \in \mathbb{R}^p })（所有可能的预测器），等价于(\Phi)零空间的正交补空间(Ker(\Phi)^\perp)（线性代数中 “列空间与零空间正交” 的推论）；
2. 最优性条件推导：若w是所有环境的最优分类器，则(\Phi \nabla R^e(\Phi^\top w) = 0)（梯度为零），即(\nabla R^e(v) \in Ker(\Phi))；
3. 正交性与分解：由(v \in Ker(\Phi)^\perp)和(\nabla R^e(v) \in Ker(\Phi))，可得(v^\top \nabla R^e(v) = 0)—— 此时可构造秩 1 的(\Phi)，让(v = \Phi^\top \cdot 1.0)，实现等价分解。

证明意义

为 IRMv1 的 “固定(w=1.0)” 提供理论依据：无需优化w，仅通过(\Phi)的非线性特征提取，就能覆盖所有线性不变预测器的表达能力，既简化优化（避免参数冗余），又不损失模型能力。

B.3 定理 9 的证明：IRM 泛化到所有环境的条件

定理 9 回顾

若训练环境满足 “r阶线性一般位置”，且 IRM 学到秩为r的表示(\Phi)，则(\Phi)引出的预测器在所有环境中都不变（即分布外泛化）。

证明核心逻辑

1. 反证法构造矛盾：假设(\Phi^\top w \neq \tilde{S}^\top \gamma)（(\tilde{S}^\top \gamma)是真实因果预测器），则由线性一般位置假设，(dim(span{ q_e }) > d-r)（(q_e)是违反正规方程的残差向量）；
2. 零空间维度冲突：但(q_e \in Ker(\Phi))（由 IRM 的优化条件），若(dim(span{ q_e }) > d-r)，则(dim(Ker(\Phi)) > d-r)—— 与(\Phi)秩为r（(dim(Ker(\Phi)) = d-r)）矛盾；
3. 结论推导：因此假设不成立，(\Phi^\top w = \tilde{S}^\top \gamma)，即预测器在所有环境中不变。

证明意义

首次从数学上证明 “IRM 的不变性可迁移到未见过的环境”，将 IRM 从 “工程算法” 提升为 “有泛化保证的理论范式”。

B.4 定理 10 的证明：线性一般位置的测度为零

证明核心逻辑

1. 流形横截性理论：定义映射(G(x))描述环境协方差与残差的关系，证明(G(x))的像集W与 “低秩矩阵集(LR(m,d,k))” 横截（要么不相交，要么相交维度合理）；
2. 维度计数矛盾：若(k < d-r)且(m > \frac{d}{r} + d-r)，则(dim(W) + dim(LR(m,d,k)) - dim(\mathbb{R}^{m×d}) < 0)—— 横截相交的维度为负，不可能发生，故W与(LR(m,d,k))不相交；
3. 测度为零结论：不满足线性一般位置的协方差矩阵集是(LR(m,d,k))的子集，故测度为零。

附录 C：领域自适应（DA）的失败案例

附录 C 是 IRM 的 “竞品对比分析”，通过具体场景证明传统领域自适应方法（如 ADA、C-ADA）无法学习因果不变性，凸显 IRM 的优势。

核心观点

领域自适应的核心思路（匹配特征分布(P(\Phi(X^e)))）与 IRM 的目标（匹配条件分布(P(Y|\Phi(X^e)))）本质冲突 —— 前者追求 “表面分布一致”，后者追求 “因果关联不变”，导致 DA 在多种场景下失效。

案例 1：标签分布变化导致 DA 泛化灾难

场景设定

• 源环境(e_s)：(P(Y=1) = 1/2)（正样本占 50%）；
• 目标环境(e_t)：(P(Y=1) = 9/10)（正样本占 90%）；
• 真实因果关联：(P(Y|X))跨环境不变（X是 Y 的因）。

DA 的失败过程

1. ADA 强制(P(\Phi(X^{e_s})) = P(\Phi(X^{e_t})))，间接导致预测分布(P(\hat{Y}^{e_s}) = P(\hat{Y}^{e_t}))（(\hat{Y} = w(\Phi(X)))）；
2. 目标环境中 90% 是正样本，但模型预测正样本占比被强制为 50%，大量正样本被误判，准确率仅 20%（低于随机猜测）；
3. 对比 IRM/ERM：ERM 因(P(Y|X))不变，在目标环境准确率达 80%，IRM 泛化能力更优。

失败根源

DA 混淆 “边际分布不变” 与 “条件分布不变”—— 真实不变性是(P(Y|X))，而非(P(X))，强制(P(X))一致会破坏因果关联。

案例 2：条件领域自适应（C-ADA）无法识别真实不变性

C-ADA 的改进思路

按标签分组匹配分布：对每个y，强制(P(\Phi(X)|Y=y))在源 / 目标环境一致，试图解决 “标签分布变化” 问题。

失败过程（离散特征场景）

1. 数据生成：(Y^e = F(X^e) \oplus Bernoulli(p))（(F(X))是真实标签，加噪声），(P(X^e))是跨环境唯一变量；
2. 平凡表示(\Phi(x)=x)：能引出不变预测器（(P(Y|\Phi(X)))不变），但 C-ADA 需(P(\Phi(X)|Y=y))一致；
3. 测度为零结论：通过贝叶斯公式推导，满足(P(\Phi(X)|Y=y))一致的(\Phi)集合 “测度为零”——C-ADA 几乎不可能找到(\Phi(x)=x)，最终丢弃真实不变性。

失败根源

C-ADA 的 “条件分布匹配” 是过强且不必要的约束：真实不变性只需(P(Y|\Phi(X)))一致，无需(P(\Phi(X)|Y))一致，强制后者会排除有效不变表示。

DA 的共性缺陷

DA 的误差界（(Error^{e_t} \leq Error^{e_s} + Distance(\Phi(X^{e_s}), \Phi(X^{e_t})) + \lambda^)）中，(\lambda^)（最优分类器误差）被视为常数，但(\lambda^)实际依赖(\Phi)——DA 为匹配分布可能导致(\lambda^)增大，最终泛化性能下降，而 IRM 直接优化(P(Y|\Phi(X)))，避开这一陷阱。

附录 D：IRM 的 PyTorch 最小实现

附录 D 是 “工程落地指南”，提供极简代码示例，展示 IRMv1 的核心逻辑（双小批量无偏估算惩罚项、端到端训练），帮助读者快速复现算法。

核心代码模块解析

1. 惩罚项计算函数（compute_penalty）

def compute_penalty(losses, dummy_w):
    # losses：2b个样本的损失（前b个来自B1，后b个来自B2）
    # dummy_w：虚拟标量w=1.0（用于触发梯度计算）
    g1 = grad(losses[0::2].mean(), dummy_w, create_graph=True)[0]  # B1的梯度
    g2 = grad(losses[1::2].mean(), dummy_w, create_graph=True)[0]  # B2的梯度
    return (g1 * g2).sum()  # 两两相乘求和，无偏估算梯度范数平方

• 双小批量拆分：通过 losses[0::2]和 losses[1::2]，从 2b 个样本中拆分出两个独立小批量 B1、B2；
• 梯度计算：create_graph=True保留计算图，确保惩罚项的梯度能反向传播到(\Phi)；
• 无偏估算：(g1 \cdot g2)的期望等于(| \nabla R^e |^2)，解决单个小批量的偏差问题。

2. 数据生成函数（example_1）

模拟正文示例 1 的线性场景：(X_1 \sim \mathcal{N}(0, env^2))，(Y = X_1 + \mathcal{N}(0, env^2))，(X_2 = Y + \mathcal{N}(0, 1))，返回输入(X=(X_1,X_2))和目标Y。

3. 训练循环

• 模型参数：(\Phi)用 4×1 矩阵（输入 4 维：(X_1)的 2 维扩展 +(X_2)的 2 维扩展），dummy_w=1.0固定；
• 损失计算：经验风险项（MSE）+ 惩罚项（(\lambda=1)，通过 1e-5 * error + penalty平衡量级）；
• 优化目标：仅优化(\Phi)，dummy_w仅用于求导，不实际更新。

代码意义

验证 IRMv1 的可实现性：仅需几十行代码就能实现核心逻辑，且训练后(\Phi)的权重会向(X_1)倾斜（忽略(X_2)的虚假关联），证明 IRM 在工程上简洁且有效。

附录整体价值总结

附录	核心作用	对正文的支撑
A	理论保障	证明 “线性一般位置” 是自然属性，消除假设苛刻性担忧
B	逻辑严谨	推导核心命题 / 定理，确保 IRM 的理论无漏洞
C	竞品对比	凸显 IRM 相对于 DA 的优势，明确 IRM 的定位
D	工程落地	提供极简实现，降低复现门槛，验证算法可行性

四个附录从 “理论 - 逻辑 - 对比 - 工程” 全方位支撑正文，使 IRM 不仅是 “想法”，更是 “有证明、有优势、可实现” 的完整泛化范式。

---

名词解析

1 正规方程

下面从 “线性回归的目标→正规方程的推导→公式含义→与 IRM 的关联→优缺点” 五个维度，用通俗语言 + 简单公式拆解，完全避开复杂的线性代数推导门槛。

一、先明确背景：为什么需要正规方程？

正规方程的应用场景是线性回归—— 比如 “用(X_1)（奶牛形状）和(X_2)（背景颜色）预测Y（是否是奶牛）”，线性回归的模型是：(\hat{Y} = \theta_0 + \theta_1 X_1 + \theta_2 X_2)其中(\theta_0)（截距）、(\theta_1)（(X_1)的系数）、(\theta_2)（(X_2)的系数）是我们要学的 “最优参数”。

线性回归的目标是最小化 “预测值(\hat{Y})和真实值Y的均方误差”，即：(L(\theta) = \frac{1}{n} \sum_{i=1}^n (Y_i - \hat{Y}i)^2 = \frac{1}{n} \sum{i=1}^n (Y_i - (\theta_0 + \theta_1 X_{i1} + \theta_2 X_{i2}))^2)

要找最小化(L(\theta))的(\theta)，有两种方法：

1. 梯度下降：通过多次迭代，逐步调整(\theta)直到误差收敛（适合数据量大、特征多的场景）；
2. 正规方程：直接通过数学推导，解出(\theta)的解析解（适合数据量小、特征少的场景，也方便理论分析）。

文档第三部分用正规方程，正是因为它能提供 “线性分类器最优的严格条件”—— 这是设计(\mathbb{D}_{lin})惩罚项的关键。

二、正规方程怎么来的？—— 核心是 “导数为零找极值”

要找到让误差(L(\theta))最小的(\theta)，数学上的核心思路是：对(L(\theta))关于每个(\theta)求偏导数，令导数等于 0，解方程组得到(\theta)。

为了简化计算，我们先把 “带截距的模型” 转化为 “矩阵形式”（这是正规方程的标准写法）：

1. 给每个样本增加一列 “1”（对应截距(\theta_0)），把特征矩阵X扩展为(n \times (d+1))的矩阵（n是样本数，d是特征数）；
2. 把参数(\theta = [\theta_0, \theta_1, \theta_2]^T)写成向量形式；
3. 预测值(\hat{Y} = X \cdot \theta)（矩阵乘法，代替逐个样本计算）；
4. 误差(L(\theta) = \frac{1}{n} | Y - X\theta |^2)（(| \cdot |^2)是 “平方和”，简化写法）。

接下来对(L(\theta))关于(\theta)求导（利用矩阵求导法则），令导数等于 0，整理后就能得到：(\boxed{X^T X \theta = X^T Y})这就是正规方程的核心等式。再把(\theta)解出来（假设(X^T X)可逆）：(\boxed{\theta = (X^T X)^{-1} X^T Y})

三、正规方程的通俗含义：“最优系数的公式”

上面的公式看起来抽象，我们用 “文档中的线性分类器场景” 翻译一下：在文档第三部分，线性分类器的参数是w（对应这里的(\theta)），数据表示是(\Phi(X))（对应这里的X），目标变量是Y。因此，文档中 “基于(\Phi(X))的最优线性分类器(w_\Phi^e)”，用正规方程写出来就是：(w_\Phi^e = \left( \mathbb{E}[\Phi(X^e)\Phi(X^e)^T] \right)^{-1} \mathbb{E}[\Phi(X^e)Y^e])（文档里用 “期望(\mathbb{E})” 代替 “样本平均”，是从统计理论角度的严格写法，和上面的样本形式本质一致 —— 把(X^T X)理解为 “样本特征的协方差相关矩阵”，(X^T Y)理解为 “样本特征与目标的协方差向量”）。

这个公式的通俗含义是：只要把特征(\Phi(X))和目标Y代入，通过一次矩阵运算，就能直接得到 “让均方误差最小” 的最优分类器(w_\Phi^e)—— 这就是线性回归的 “最优解”。

四、为什么文档第三部分这么重视正规方程？—— 和 IRM 的关联

文档第三部分设计(\mathbb{D}_{lin})惩罚项时，核心思路就是 “绕开求逆，直接用正规方程的等式判断最优性”：

1. 正规方程的核心等式是(X^T X \theta = X^T Y)（或文档中的(\mathbb{E}[\Phi\Phi^T] w = \mathbb{E}[\Phi Y])）；
2. 对一个分类器w来说，“是否是最优” 等价于 “是否满足这个等式”—— 如果满足，说明w是最优的；如果不满足，“等式两边的差距” 就是 “w离最优的距离”；
3. 因此，文档中的(\mathbb{D}{lin})惩罚项直接用 “这个差距的平方” 来定义：(\mathbb{D}{lin}(w,\Phi,e) = \left| \mathbb{E}[\Phi(X^e)\Phi(X^e)^T] w - \mathbb{E}[\Phi(X^e)Y^e] \right|^2)

这一设计完美解决了(\mathbb{D}_{dist})的缺陷：

• 不用计算((X^T X)^{-1})（避免矩阵求逆导致的数值爆炸和不连续性）；
• 直接用 “等式差距” 衡量最优性，保证惩罚项光滑可导，适合梯度下降优化。

五、正规方程的优缺点：什么时候用？

理解正规方程的适用场景，能更清楚文档为什么这么设计：

优点	缺点
1. 直接出最优解，不用迭代（梯度下降要调学习率、多次迭代）；	1. 要计算((X^T X)^{-1})，时间复杂度是(O(d^3))（d是特征数）—— 特征多（比如(d>10^4)）时计算量爆炸；
2. 理论意义明确，是 “线性回归最优解” 的严格数学表达；	2. 当(X^T X)不可逆（比如特征线性相关）时，无法求解（需要加正则化）。
3. 文档中可直接用来设计惩罚项，避开数值问题。

文档中用正规方程，正是利用了它的 “理论严格性”—— 作为 “最优分类器的判断标准”，而不是用它来实际求解大规模数据的系数（实际 IRM 训练用的是梯度下降，正规方程只是理论工具）。

总结：正规方程的核心定位

对理解 IRM 来说，正规方程的核心作用是 “线性分类器最优性的标尺”：

• 它告诉我们 “什么样的w是最优的”（满足(\mathbb{E}[\Phi\Phi^T] w = \mathbb{E}[\Phi Y])）；
• 文档基于这个标尺，设计了(\mathbb{D}_{lin})惩罚项，让模型能通过梯度下降学习 “接近最优的不变分类器”；
• 它是连接 “线性回归理论” 和 “IRM 算法设计” 的关键桥梁，也是理解(\mathbb{D}_{lin})为什么能稳定优化的核心。

简单说：正规方程本身是线性回归的 “最优解公式”，但在 IRM 中，它被用作 “判断不变性的工具”—— 这是文档第三部分用它的核心原因。

2 缩放作弊

第一步：先构造一个简单场景（简化版示例 1）

为了避免复杂的矩阵运算，我们用一维特征简化（本质和文档中的高维场景一致）：

• 目标：基于特征X预测Y，真实因果关系是(Y = X + \text{噪声})（X是 “不变因果特征”，比如奶牛形状）；

• 数据表示(\Phi)：初始设为(\Phi(X) = X)（正确提取因果特征）；

• 分类器w：初始设为(w=1)（正确的权重，预测结果(\hat{Y} = w \cdot \Phi(X) = 1 \cdot X = X)，接近真实Y）；

• 不变性惩罚项：用文档中的(\mathbb{D}{lin})（简化为标量版，因为(\Phi)是一维）：(\mathbb{D}{lin}(w,\Phi) = \left| \mathbb{E}[\Phi^2] \cdot w - \mathbb{E}[\Phi Y] \right|^2)

  （标量版中，矩阵乘法变成普通乘法，范数变成绝对值，本质不变）。

先计算初始合理状态的数值（假设统计期望已知，用具体数代替）：

• 设(\mathbb{E}[\Phi^2] = \mathbb{E}[X^2] = 2)（X的二阶矩）；
• 设(\mathbb{E}[\Phi Y] = \mathbb{E}[X \cdot (X+\text{噪声})] = \mathbb{E}[X^2] = 2)（噪声与X独立，期望为 0）；
• 此时(\mathbb{D}_{lin}(w=1, \Phi=X) = |2 \cdot 1 - 2|^2 = 0)（惩罚项为 0，说明(w=1)是最优分类器，符合不变性要求）。

第二步：模拟 “缩放作弊”——Φ 缩小、w 放大

现在，模型开始 “作弊”：选择一个很小的缩放系数(\gamma)（比如(\gamma=0.01)，即缩小 100 倍），做两个操作：

1. 数据表示缩放：(\Phi' = \gamma \cdot \Phi = 0.01 \cdot X)（原来的(\Phi(X)=X)变成(\Phi'(X)=0.01X)，缩小 100 倍）；
2. 分类器缩放：(w' = \frac{w}{\gamma} = \frac{1}{0.01} = 100)（原来的(w=1)变成(w'=100)，放大 100 倍）。

关键观察 1：预测结果不变（模型 “假装” 在正常预测）

缩放后的预测结果是：(\hat{Y}' = w' \cdot \Phi'(X) = 100 \cdot (0.01X) = X)和原来的(\hat{Y}=X)完全一样！—— 模型的预测能力没变化，经验风险（预测误差）也没变化，看起来 “一切正常”。

关键观察 2：不变性惩罚项趋近于 0（模型 “逃避” 不变性要求）

现在计算缩放后的(\mathbb{D}_{lin}(w', \Phi'))：

• 先算(\mathbb{E}[\Phi'^2] = \mathbb{E}[(0.01X)^2] = 0.0001 \cdot \mathbb{E}[X^2] = 0.0001 \cdot 2 = 0.0002)；
• 再算(\mathbb{E}[\Phi' Y] = \mathbb{E}[(0.01X) \cdot Y] = 0.01 \cdot \mathbb{E}[XY] = 0.01 \cdot 2 = 0.02)；
• 代入(\mathbb{D}{lin})公式：(\mathbb{D}{lin}(w'=100, \Phi'=0.01X) = |0.0002 \cdot 100 - 0.02|^2 = |0.02 - 0.02|^2 = 0)

如果把(\gamma)调得更小（比如(\gamma=0.001)，缩小 1000 倍）：

• (\Phi''=0.001X)，(w''=1000)；
• (\mathbb{E}[\Phi''^2] = 0.000001 \cdot 2 = 0.000002)；
• (\mathbb{E}[\Phi'' Y] = 0.001 \cdot 2 = 0.002)；
• (\mathbb{D}_{lin} = |0.000002 \cdot 1000 - 0.002|^2 = |0.002 - 0.002|^2 = 0)。

结论：无论(\gamma)多小（(\Phi)多小），只要w按(1/\gamma)放大，惩罚项(\mathbb{D}_{lin})始终为 0—— 模型用 “缩放” 操作，让惩罚项 “失效” 了。

第三步：为什么惩罚项会 “失效”？（公式本质拆解）

从数学上看，“缩放作弊” 能让惩罚项趋近于 0，是因为(\mathbb{D}_{lin})的公式结构和 “(\Phi)、w的缩放关系” 刚好抵消。

我们用通用的缩放操作（(\Phi'=\gamma\Phi)，(w'=w/\gamma)）代入(\mathbb{D}{lin})的标量版公式：(\mathbb{D}{lin}(w', \Phi') = \left| \mathbb{E}[(\gamma\Phi)^2] \cdot \frac{w}{\gamma} - \mathbb{E}[(\gamma\Phi) Y] \right|^2)化简里面的项：

• 第一项：(\mathbb{E}[\gamma^2 \Phi^2] \cdot \frac{w}{\gamma} = \gamma^2 \cdot \mathbb{E}[\Phi^2] \cdot \frac{w}{\gamma} = \gamma \cdot \mathbb{E}[\Phi^2] \cdot w)；
• 第二项：(\mathbb{E}[\gamma\Phi Y] = \gamma \cdot \mathbb{E}[\Phi Y])；

因此：(\mathbb{D}_{lin}(w', \Phi') = \left| \gamma \cdot (\mathbb{E}[\Phi^2] w - \mathbb{E}[\Phi Y]) \right|^2 = \gamma^2 \cdot \left| \mathbb{E}[\Phi^2] w - \mathbb{E}[\Phi Y] \right|^2)

当(\gamma)趋近于 0 时（(\Phi)无限缩小），(\gamma^2)也趋近于 0—— 不管原来的(\left| \mathbb{E}[\Phi^2] w - \mathbb{E}[\Phi Y] \right|^2)是多少，最终(\mathbb{D}_{lin})都会趋近于 0。

这就是作弊的 “数学漏洞”：模型只要不断缩小(\Phi)、放大w，就能让不变性惩罚项无限趋近于 0，相当于 “绕过了不变性要求”。

第四步：作弊的危害 —— 模型退化成 ERM，学不到不变性

IRM 的目标函数是 “损失 = 经验风险 +λ・惩罚项”。当惩罚项趋近于 0 时，目标函数就近似为 “仅最小化经验风险”—— 这和普通的 ERM 完全一样！

回到 “奶牛骆驼分类” 的例子：

• 作弊前：模型需要学习 “Φ 提取形状特征，w=1 最优”，惩罚项保证不变性；
• 作弊后：模型发现 “缩小 Φ（比如 Φ 同时提取形状和背景）、放大 w”，既能让预测结果（比如 “背景颜色→标签”）的经验风险很小，又能让惩罚项趋近于 0—— 于是模型就会偷懒，只学 “背景颜色” 这种虚假关联，而不学 “形状” 这种不变特征；
• 最终后果：在训练环境中误差很小，但在新环境（比如沙滩奶牛）中彻底翻车 —— 和 ERM 的泛化失败完全一样，IRM 的 “不变性优势” 彻底消失。

总结：固定 w=1.0 的本质 —— 堵上 “缩放作弊” 的漏洞

不固定w时，“Φ 和 w 的缩放冗余” 给了模型 “钻空子” 的机会：用缩放操作让惩罚项失效，逃避学习不变性的任务。

而固定(w=1.0)，相当于强行消除了这种冗余：

• 此时w不能再放大，模型无法通过 “缩放 w” 来抵消 “Φ 缩小” 的影响；
• 要让惩罚项变小，模型只能调整(\Phi)，让(\Phi)本身提取出 “能让 w=1.0 最优的不变特征”（比如形状）—— 这才是 IRM 真正想让模型做的事。

简单说：固定 w=1.0，就是 “断了模型作弊的后路”，逼着它必须学习不变性，而不是靠缩放耍小聪明。

3. 固定最优分类器W为标量1.0

一、先明确：“固定标量w” 是 “三步简化” 的最终结果，不是一开始的假设

第三部分对w的处理是逐步收敛的，不是一开始就固定为标量。整个过程分三个阶段，你的理解对应最后一个阶段：

阶段	对w的处理	核心问题	后续改进方向
1. 理想 IRM 模型	w是 “每个环境下独立的最优分类器”（比如环境 1 的(w_1)、环境 2 的(w_2)）	双层优化，计算量极大（每个环境要解一次内层w的优化）	把 “硬约束” 改成 “软惩罚”，合并w和(\Phi)的优化
2. 带惩罚项的模型（(L_{IRM})）	w是 “共享的线性分类器”（不再分环境，但仍是向量，比如(w=(w_1,w_2))）	参数冗余（(\gamma\Phi)和(w/\gamma)效果一样，导致惩罚项失效）	固定w的形式，消除冗余
3. 最终 IRMv1 模型	w固定为 “标量 1.0”（不再是向量，所有环境共享这一个标量）	会不会限制表示能力？	用定理 4 证明 “等价性”，用(\Phi)的灵活性弥补

简单说：“固定标量w” 是为了解决 “参数冗余” 问题 —— 如果不固定w，模型会通过 “缩放(\Phi)和w” 作弊（比如(\Phi)缩小 100 倍，w放大 100 倍，预测结果不变但惩罚项趋近于 0），无法学到真正的不变性。

二、关键证明：为什么 “固定标量(w=1.0)” 就够了？（定理 4 的通俗解读）

文档用 “定理 4” 严格证明了：任何线性不变预测器，都能分解成 “秩 1 的数据表示(\Phi)”+“标量分类器(w=1.0)”—— 这是 “固定标量w” 的核心理论支撑，也是最容易被忽略的关键。

我们用第二部分的 “奶牛分类示例” 具象化这个证明：假设 “跨环境的最优不变预测器” 是(\hat{Y} = 1 \cdot X_1 + 0 \cdot X_2)（只看形状(X_1)，不看背景(X_2)），这个预测器可以拆成两种等价形式：

形式	数据表示(\Phi)	分类器w	最终预测器(w \circ \Phi)	本质
原形式（向量w）	(\Phi(X) = (X_1, X_2))（提取两个特征）	(w=(1, 0))（向量，给(X_1)权重 1，(X_2)权重 0）	(1 \cdot X_1 + 0 \cdot X_2)	用w的权重筛选有用特征
等价形式（标量w）	(\Phi(X) = X_1)（只提取有用的(X_1)特征，秩 1）	(w=1.0)（标量，直接输出(\Phi(X))）	(1.0 \cdot X_1)	用(\Phi)直接提取有用特征，w仅做 “传递”

这两种形式的预测结果完全一致，但第二种形式有个巨大优势：不用优化w，只需优化(\Phi)，让(\Phi)提取出 “能让(w=1.0)最优的特征”。

定理 4 进一步推广了这个结论：哪怕是更复杂的线性不变预测器（比如(\hat{Y} = 2 \cdot X_1 + 3 \cdot X_3)），也能拆成 “(\Phi(X) = 2X_1 + 3X_3)”+“(w=1.0)”—— 也就是说，w的 “权重分配功能” 可以完全转移给(\Phi)，w本身只需做 “标量传递”，固定为 1.0 不会损失任何表示能力。

三、固定(w=1.0)后，怎么保证 “在所有环境下都是最优分类器”？

这是最核心的疑问：既然w固定了，怎么确保它在每个环境下都满足 “最优”？答案是：把 “优化w的任务” 转移给了(\Phi)，通过惩罚项倒逼(\Phi)学习到 “让(w=1.0)最优的特征”。

具体来说，IRMv1 的目标函数通过两部分协同实现这一点：

1. 经验风险项（(\sum R^e(\Phi))）：保证(\Phi)的预测结果准 —— 即(1.0 \cdot \Phi(X) = \Phi(X))能接近真实Y，这是 “最优” 的基础；
2. 不变性惩罚项（(\lambda \cdot |\nabla_{w=1.0} R^e(w \cdot \Phi)|^2)）：保证(w=1.0)是 “基于(\Phi)的最优分类器”——
   • 回顾正规方程：“w最优” 等价于 “(\mathbb{E}[\Phi\Phi^T] w = \mathbb{E}[\Phi Y])”；
   • 对固定的(w=1.0)，惩罚项衡量的正是 “(w=1.0)违反这个等式的程度”（梯度越小，违反程度越低，(w=1.0)越接近最优）；
   • 模型通过梯度下降优化(\Phi)，会同时最小化 “预测误差” 和 “违反最优条件的程度”，最终让(\Phi)满足：对所有环境e，(\mathbb{E}[\Phi\Phi^T] \cdot 1.0 = \mathbb{E}[\Phi Y])—— 即(w=1.0)在所有环境下都是最优分类器。

举个通俗例子：

• 环境 1（牧场）：最优特征是 “绿色背景 + 四条腿”，但(w=1.0)固定；
• 环境 2（沙滩）：最优特征是 “黄色背景 + 四条腿”，但(w=1.0)固定；
• 模型会调整(\Phi)，最终提取出 “四条腿” 这个跨环境不变的特征 —— 此时(w=1.0)在两个环境下，基于 “四条腿” 特征的预测都是最优的（因为 “四条腿” 和Y的关联不变）。

四、误区澄清：固定标量w会不会限制 “非线性不变性”？

用户可能会担心：如果真实的不变预测器是非线性的（比如(\hat{Y} = \Phi(X)^2)），固定线性的(w=1.0)会不会抓不到这种非线性？

文档第三部分 3.3 节专门回应了这个问题，核心结论是：不会限制，因为(\Phi)可以是非线性的。比如真实不变预测器是(\hat{Y} = (\Phi_0(X))^2)（(\Phi_0(X))是 “四条腿” 特征），我们可以让 IRMv1 的(\Phi(X) = (\Phi_0(X))^2)—— 此时(w=1.0 \cdot \Phi(X) = (\Phi_0(X))^2)，完全等价于真实的非线性预测器。

也就是说，w的线性与否不重要，重要的是(\Phi)的灵活性—— 只要(\Phi)用深度神经网络等非线性模型，IRMv1 就能捕捉到非线性的不变关联。固定(w=1.0)只是 “简化优化”，不会限制模型的表达能力。

总结：固定标量(w=1.0)是 “简化优化” 与 “表示能力” 的平衡

第三部分对w的处理，本质是一次非常巧妙的 “问题转化”：

• 不直接优化 “每个环境的最优w”（复杂、冗余）；
• 而是把 “w的最优性要求” 转化为 “对(\Phi)的约束”（通过惩罚项）；
• 最终固定(w=1.0)，让优化目标从 “双层（(\Phi,w)）” 变成 “单层（(\Phi)）”，既解决了计算难题，又不损失不变性的核心要求。

你的理解抓住了这一简化的关键 —— 正是因为w被固定为标量，IRM 才从理论上的 “双层优化” 变成了工程上可落地的 “梯度下降训练”，这也是 IRMv1 能实际训练的核心原因。

4. 实现细节：无偏估计

一、先明确：实现的核心目标是什么？

IRMv1 的目标函数需要计算两部分，实现细节主要针对第二部分（不变性惩罚项）：(\min {\Phi} \underbrace{\sum{e \in \mathcal{E}{tr}} R^e(\Phi)}{\text{1. 经验风险项（好算）}} + \lambda \cdot \underbrace{\sum_{e \in \mathcal{E}{tr}} \left| \nabla{w|w=1.0} R^e(w \cdot \Phi) \right|^2}_{\text{2. 不变性惩罚项（难算，实现细节的核心）}})

1. 经验风险项（简单回顾，不是重点）

• 含义：模型在每个环境的预测误差（比如分类任务的交叉熵、回归任务的均方误差）；
• 计算方式：对每个环境e，取一个小批量样本((X^e, Y^e))，用模型(\Phi)输出预测值(\Phi(X^e))，直接计算损失（比如 cross_entropy(Φ(X^e), Y^e)），求和即可。

这部分和普通神经网络训练完全一致，没有特殊细节，重点在 “不变性惩罚项”。

2. 不变性惩罚项（实现难点）

• 含义：衡量 “固定标量(w=1.0)时，每个环境下的风险(R^e(w \cdot \Phi))对w的梯度范数平方”—— 梯度越小，说明(w=1.0)越接近该环境的最优分类器，不变性越强；
• 核心难题：公式中的(\nabla_{w|w=1.0} R^e(w \cdot \Phi))是期望梯度（需要用整个环境的所有数据计算），但实际训练中只能用 “小批量样本” 估算 —— 如何用小批量无偏估算这个期望梯度的范数平方？

这就是 “实现细节” 要解决的核心问题：用两个独立小批量，无偏估算 “梯度范数平方”。

二、核心难题：为什么不能用 “单个小批量” 估算？

先理解 “梯度范数平方” 的数学含义：对环境e，惩罚项是(\left| \nabla_{w=1.0} R^e(w \cdot \Phi) \right|^2 = \left| \mathbb{E}{(X,Y) \sim e} \left[ \nabla{w=1.0} \ell(w \cdot \Phi(X), Y) \right] \right|^2)其中(\ell)是单个样本的损失（比如交叉熵、MSE），(\mathbb{E})表示对环境e的所有样本取期望。

如果用单个小批量估算（比如取一批样本B，计算平均梯度后平方）：(\text{错误估算} \approx \left| \frac{1}{|B|} \sum_{(X,Y) \in B} \nabla_{w=1.0} \ell(w \cdot \Phi(X), Y) \right|^2)会出现偏差—— 因为数学上 “期望的平方≠平方的期望”（(\mathbb{E}[a]^2 \neq \mathbb{E}[a^2])）。

举个简单例子：假设a是随机变量（比如单个样本的梯度），(\mathbb{E}[a] = 0)（梯度期望为 0，模型接近最优），但(\mathbb{E}[a^2] = 2)（单个样本梯度有波动）。此时：

• 真实的 “梯度范数平方” 是(\mathbb{E}[a]^2 = 0)；
• 用单个小批量估算：若批量中样本的平均梯度是(\frac{a_1+a_2}{2})，平方后可能是((\frac{1+(-1)}{2})^2 = 0)（偶尔对），也可能是((\frac{2+0}{2})^2 = 1)（有偏差）—— 无法稳定无偏估算。

这就是为什么文档要设计 “用两个独立小批量” 的方案：规避偏差，保证估算的无偏性。

三、解决方案：用 “两个独立小批量” 无偏估算

文档给出的核心技巧是：对每个环境e，抽取两个独立的小批量（记为(B_1 = {(X_1,Y_1), ..., (X_b,Y_b)})和(B_2 = {(X_1',Y_1'), ..., (X_b',Y_b')})，批量大小都是b），用以下公式估算 “梯度范数平方”：(\widehat{\left| \nabla_{w=1.0} R^e \right|^2} = \frac{1}{b} \sum_{k=1}^b \left[ \nabla_{w=1.0} \ell(w \cdot \Phi(X_k), Y_k) \cdot \nabla_{w=1.0} \ell(w \cdot \Phi(X_k'), Y_k') \right])

1. 为什么这个公式是 “无偏” 的？（数学直觉）

我们用期望的线性性质验证：(\mathbb{E}\left[ \frac{1}{b} \sum_{k=1}^b g_k \cdot g_k' \right] = \frac{1}{b} \sum_{k=1}^b \mathbb{E}[g_k \cdot g_k'])其中(g_k = \nabla_{w=1.0} \ell(w \cdot \Phi(X_k), Y_k))（(B_1)中第k个样本的梯度），(g_k' = \nabla_{w=1.0} \ell(w \cdot \Phi(X_k'), Y_k'))（(B_2)中第k个样本的梯度）。

由于(B_1)和(B_2)独立，(\mathbb{E}[g_k \cdot g_k'] = \mathbb{E}[g_k] \cdot \mathbb{E}[g_k'])（独立变量的期望乘积 = 乘积的期望）。而(\mathbb{E}[g_k] = \nabla_{w=1.0} R^e)（单个样本梯度的期望就是环境的整体梯度），因此：(\mathbb{E}\left[ \frac{1}{b} \sum_{k=1}^b g_k \cdot g_k' \right] = \frac{1}{b} \sum_{k=1}^b \mathbb{E}[g_k] \cdot \mathbb{E}[g_k'] = \left( \nabla_{w=1.0} R^e \right) \cdot \left( \nabla_{w=1.0} R^e \right) = \left| \nabla_{w=1.0} R^e \right|^2)

这就证明了：用两个独立小批量的 “样本梯度两两相乘再平均”，能无偏估算真实的 “梯度范数平方”—— 解决了单个小批量的偏差问题。

2. 用具体例子理解：分类任务的梯度计算

以 “彩色 MNIST 分类任务” 为例（交叉熵损失），进一步拆解 “单个样本的梯度(g_k)” 怎么算：

• 模型结构：(\Phi)是一个深度神经网络（比如 MLP），输入是彩色 MNIST 图像X，输出是 “logit 值”（记为(h = \Phi(X))，因为(w=1.0)固定，预测 logit 就是(w \cdot \Phi(X) = h)）；
• 单个样本损失：交叉熵损失(\ell(h, Y) = -Y \cdot \log(\sigma(h)) - (1-Y) \cdot \log(1-\sigma(h)))，其中(\sigma(h))是 sigmoid 函数（二分类）；
• 对w的梯度：由于(h = w \cdot \Phi(X))，当(w=1.0)时，(\frac{\partial h}{\partial w} = \Phi(X))。根据链式法则：(\nabla_{w=1.0} \ell(w \cdot \Phi(X), Y) = \frac{\partial \ell}{\partial h} \cdot \frac{\partial h}{\partial w} = (\sigma(h) - Y) \cdot \Phi(X))

也就是说，“单个样本的梯度(g_k)” 就是 “(预测概率 - 真实标签) × 模型输出(\Phi(X_k))”—— 这是代码中可以直接计算的量。

四、对应代码：从公式到 PyTorch 实现（结合文档附录 D）

文档附录 D 给出了 PyTorch 实现的核心代码，我们结合上面的逻辑，逐行拆解关键部分，让你看到 “实现细节” 如何落地：

1. 核心函数：计算单个环境的不变性惩罚项

def compute_penalty(losses, dummy_w):
    # losses: 单个环境的两个小批量损失（shape: [2b]，前b个来自B1，后b个来自B2）
    # dummy_w: 固定的标量w=1.0（PyTorch参数，requires_grad=True，用于求导）
  
    # 1. 从losses中拆分两个独立小批量的损失：B1（0::2，步长2取前b个）、B2（1::2，步长2取后b个）
    loss1 = losses[0::2].mean()  # B1的平均损失
    loss2 = losses[1::2].mean()  # B2的平均损失
  
    # 2. 计算B1对dummy_w的梯度g1，B2对dummy_w的梯度g2（create_graph=True保留计算图，用于后续反向传播）
    g1 = torch.autograd.grad(loss1, dummy_w, create_graph=True)[0]
    g2 = torch.autograd.grad(loss2, dummy_w, create_graph=True)[0]
  
    # 3. 两个梯度逐元素相乘后求和：对应公式中的“1/b ∑g_k·g_k'”（批量平均已在loss1/loss2中完成）
    return (g1 * g2).sum()

2. 训练循环：整合所有环境的损失和惩罚项

# 1. 初始化模型和参数
phi = torch.nn.Sequential(  # 数据表示Φ：MLP网络（输出logit，即w·Φ(X)，w=1.0固定）
    torch.nn.Linear(784*3, 256),  # 彩色MNIST：3通道×784像素=2352输入特征
    torch.nn.ReLU(),
    torch.nn.Linear(256, 1)       # 输出1个logit值（二分类）
)
dummy_w = torch.nn.Parameter(torch.Tensor([1.0]), requires_grad=True)  # 固定w=1.0，需求导
opt = torch.optim.SGD(list(phi.parameters()) + [dummy_w], lr=1e-3)  # 优化器：同时优化Φ和dummy_w（w实际不变，仅用于求导）
mse = torch.nn.MSELoss(reduction="none")  # 损失函数（示例用MSE，分类用CrossEntropyLoss）

# 2. 准备多环境数据（比如两个训练环境：env1, env2）
environments = [env1_data, env2_data]  # 每个环境数据是(X, Y)，X: [n, 2352], Y: [n, 1]

# 3. 训练循环
for iteration in range(50000):
    total_error = 0.0
    total_penalty = 0.0
  
    # 对每个环境单独计算误差和惩罚项
    for x_e, y_e in environments:
        # 3.1 抽取该环境的一个大批量，再拆成两个独立小批量（通过随机打乱+分割实现）
        batch_size = 64  # 单个小批量大小b=64，大批量大小=2b=128
        perm = torch.randperm(len(x_e))  # 随机打乱样本索引
        x_batch = x_e[perm[:2*batch_size]]  # 取前128个样本作为大批量
        y_batch = y_e[perm[:2*batch_size]]
  
        # 3.2 计算该大批量的损失（每个样本的损失，reduction="none"保留单个损失）
        h = phi(x_batch)  # 模型输出Φ(X)，即w·Φ(X)（w=1.0）
        losses = mse(h * dummy_w, y_batch)  # 单个样本损失：losses.shape = [128]
  
        # 3.3 计算该环境的经验误差（大批量平均损失）
        error_e = losses.mean()
        total_error += error_e
  
        # 3.4 计算该环境的不变性惩罚项（调用compute_penalty函数）
        penalty_e = compute_penalty(losses, dummy_w)
        total_penalty += penalty_e
  
    # 3.5 计算总损失：经验风险项（乘以小系数1e-5，平衡量级） + 惩罚项
    total_loss = 1e-5 * total_error + total_penalty
  
    # 3.6 反向传播+参数更新（仅更新phi的参数，dummy_w的梯度会被计算但实际不更新，因为w固定为1.0）
    opt.zero_grad()
    total_loss.backward()
    opt.step()
  
    # 3.7 日志输出（每1000轮打印模型参数）
    if iteration % 1000 == 0:
        print("Iteration:", iteration, "Phi params:", phi[0].weight[:2])

五、关键细节补充：为什么要 “dummy_w”？

代码中引入了 “dummy_w”（虚拟的标量参数），这是实现中的一个 “技巧”，需要特别解释：

• 因为我们需要计算 “损失对 w 的梯度”，但 w 固定为 1.0，不能被优化 —— 所以用一个 “dummy_w” 作为 “梯度计算的载体”；
• 在训练中，dummy_w 的参数值始终是 1.0（不会被更新，因为它的梯度在反向传播后，优化器更新时会被 “计入”，但由于损失对 dummy_w 的梯度最终会被模型通过调整 Φ 抵消，实际 dummy_w 的值不会变）；
• 本质上，dummy_w 只是为了 “触发 PyTorch 的自动求导机制”，让我们能计算出 “损失对 w 的梯度”，而不是真的要优化 w。

总结：实现细节的核心逻辑链

1. 目标：用小批量估算 “梯度范数平方”，保证无偏性；
2. 难题：单个小批量估算有偏差（期望平方≠平方期望）；
3. 方案：对每个环境抽两个独立小批量，计算 “样本梯度两两相乘再平均”，无偏逼近真实期望；
4. 代码落地：用 PyTorch 的自动求导（torch.autograd.grad）计算两个小批量的梯度，相乘求和得到惩罚项，再和经验风险项结合优化。

简单说，实现细节的本质就是 “用两个小批量解决无偏估算问题”—— 这是 IRM 能在神经网络上训练的关键，也是从 “理论公式” 到 “实际代码” 的最后一步。

5. 线性/非线性分类器与线性/非线性不变性

一、先分清基础：线性分类器 vs 非线性分类器

分类器的 “线性 / 非线性”，描述的是 “模型输入（或特征）到预测输出的映射关系是否满足线性性质”—— 简单说，就是预测输出是否是 “输入特征的一次函数组合”。

1. 线性分类器：输入特征的一次函数

定义：对输入特征(x = (x_1, x_2, ..., x_d))（或数据表示(\Phi(x))），预测输出(\hat{y})是 “特征的线性组合 + 截距”，数学形式为：

• 回归任务（如预测房价）：(\hat{y} = w_0 + w_1 x_1 + w_2 x_2 + ... + w_d x_d)（(w_0)是截距，(w_1,...,w_d)是特征权重）；
• 分类任务（如判断是否是猫）：(\hat{y} = \sigma(w_0 + w_1 x_1 + ... + w_d x_d))（(\sigma)是激活函数，如 sigmoid、softmax，仅用于输出概率，核心特征组合仍是线性的）。

关键特点：

• 决策边界是 “线性的”（比如二维特征下是直线，三维是平面，高维是超平面）；
• 权重w是 “全局固定” 的 —— 每个特征的重要性（权重）不随输入特征的取值变化而变化。

例子：

• 文档第二部分的 “线性回归预测Y”：(\hat{Y} = \alpha_1 X_1 + \alpha_2 X_2)（无截距的线性分类器）；
• 最简单的 “感知机”：仅含一个线性层的模型，是神经网络的基础单元。

2. 非线性分类器：输入特征的非线性函数

定义：预测输出是 “输入特征的非线性函数组合”—— 通常通过 “线性操作 + 非线性激活函数” 叠加实现，数学形式没有统一表达式，但核心是 “特征之间存在乘法、平方、指数等非线性关系”。

关键特点：

• 决策边界是 “非线性的”（比如二维特征下是曲线、圆、不规则图形，高维是复杂曲面）；
• 特征的 “有效权重” 是 “动态变化” 的 —— 同一个特征在不同输入下的重要性可能不同（比如 “猫的耳朵特征” 在 “正面猫图” 和 “侧面猫图” 中的权重不同）。

例子：

• 含隐藏层的神经网络（如 MLP、CNN）：比如 “输入→线性层→ReLU→线性层→输出”，ReLU 是 nonlinear 激活函数，让整体映射变成非线性；
• 文档第五部分的 “彩色 MNIST 实验”：用 MLP 作为(\Phi)，其输出是 “像素特征的非线性组合”，属于非线性分类器。

3. 核心区别：能否捕捉特征间的复杂关联

线性分类器只能捕捉 “特征与输出的直接线性关联”（比如 “猫的耳朵长度” 与 “是猫的概率” 成正比），无法捕捉 “特征间的交互关联”（比如 “耳朵长度 + 眼睛形状” 的组合才是判断猫的关键）；而非线性分类器可以通过隐藏层和激活函数，学习到这种复杂的交互关系。

比如 “判断‘沙滩上的奶牛’”：

• 线性分类器可能只能学习 “绿色背景→奶牛”“四条腿→奶牛” 的独立关联，无法结合 “四条腿 + 沙滩背景” 的组合；
• 非线性分类器（如 CNN）可以学习 “四条腿 + 流线型身体 + 沙滩背景” 的组合特征，正确判断沙滩上的奶牛。

二、再深入：线性不变性 vs 非线性不变性

不变性的 “线性 / 非线性”，描述的是 “跨环境稳定的关联（因果规律）是否满足线性性质”—— 简单说，就是 “目标变量Y与不变特征(\Phi(x))之间的稳定关系，是一次函数还是非线性函数”。

1. 线性不变性：不变特征与 Y 的线性稳定关联

定义：存在一个跨所有环境稳定的线性关系，使得 “目标变量Y与不变特征(\Phi(x))的条件期望” 是线性的，数学形式为：(\mathbb{E}[Y^e | \Phi(x^e) = h] = w \cdot h \quad (\forall e \in E_{all}))其中h是不变特征(\Phi(x))的取值，w是跨环境固定的线性权重 —— 无论环境如何变化（如(X_2)的分布变、噪声变），这个线性关系始终成立。

例子：

• 文档第二部分的示例 1：(\mathbb{E}[Y^e | X_1^e = x_1] = x_1)（不变特征是(X_1)，Y与(X_1)的条件期望是线性的，跨环境稳定）；
• 简单物理规律：“物体下落距离s与时间t的关系”（忽略空气阻力）——(s = 0.5 g t^2)若固定g，则是s与(t^2)的线性关系（不变特征是(t^2)，线性不变性）。

2. 非线性不变性：不变特征与 Y 的非线性稳定关联

定义：跨所有环境稳定的关联是非线性的，即 “目标变量Y与不变特征(\Phi(x))的条件期望” 是 nonlinear 函数，数学形式为：(\mathbb{E}[Y^e | \Phi(x^e) = h] = f(h) \quad (\forall e \in E_{all}))其中(f(h))是非线性函数（如平方、指数、多项式等），且这个非线性函数跨环境固定 —— 环境变化只会影响 “非不变特征”（如背景、噪声），不会改变(f(h))的形式。

例子：

• 真实物理规律：“物体下落距离s与时间t的关系”（考虑空气阻力）——(s = \frac{m g}{k} (1 - e^{-\frac{k}{m} t}))（m是质量，k是阻力系数），s与t是指数非线性关系，且这个关系在 “不同高度、不同初始速度”（不同环境）下稳定；
• 图像分类：“判断是否是猫” 的不变规律 ——“猫的轮廓特征（(\Phi(x))）与‘是猫’的概率” 是非线性的（比如 “耳朵 + 眼睛 + 胡须” 的组合特征需要非线性函数才能映射到概率），且这个非线性关系在 “白天 / 夜晚、室内 / 户外”（不同环境）下稳定。

3. 核心区别：稳定关联的函数形式是否线性

线性不变性的 “稳定关联” 是 “一次函数”，可以用线性分类器直接建模；而非线性不变性的 “稳定关联” 是 “复杂函数”，必须用非线性分类器才能捕捉 —— 如果用线性分类器强行建模非线性不变性，会导致 “不变性学习失败”（比如用直线拟合曲线，无法在所有环境下稳定预测）。

三、关键关联：分类器类型与不变性类型的匹配

IRM 的核心目标是 “学习跨环境的不变性”，而分类器的类型（线性 / 非线性）决定了 “模型能否表达这种不变性”—— 两者必须匹配，否则无法学到真正的不变性。

1. 线性分类器 → 只能表达线性不变性

如果真实的不变性是非线性的（如(Y = \Phi(x)^2)），但用线性分类器（如(\hat{Y} = w \cdot \Phi(x))）建模，会出现两种问题：

• 要么 “欠拟合”：无法捕捉(\Phi(x)^2)的非线性关系，只能学到近似的线性关系（如用(\hat{Y} = 2 \Phi(x))近似(Y = \Phi(x)^2)，仅在(\Phi(x) \approx 2)时准确，其他区域误差大）；
• 要么 “依赖虚假关联”：为了降低训练误差，线性分类器会利用 “非不变特征”（如(X_2)）的线性关联，导致泛化失败（如文档中的 ERM 模型）。

例子：用线性回归预测 “(Y = x^2 + \text{噪声})”（x是不变特征，非线性不变性）：

• 线性分类器只能学到(\hat{Y} = a x + b)，无法捕捉(x^2)的关系；
• 若存在虚假特征(z = x^2)（与Y线性相关），线性分类器会优先学习(\hat{Y} = z)，但z若随环境变化（如噪声变导致z的分布变），则模型泛化失败。

2. 非线性分类器 → 可表达线性 / 非线性不变性

非线性分类器（如深度神经网络）的灵活性，使其既能表达线性不变性，也能表达非线性不变性：

• 表达线性不变性：只需让非线性分类器的 “非线性部分失效”—— 比如用 “输入→线性层→输出”（无激活函数），本质就是线性分类器；
• 表达非线性不变性：通过 “线性层 + 非线性激活函数” 叠加，学习到不变特征与Y的非线性关系 —— 比如用 MLP 学习 “(Y = \Phi(x)^2)”，只需让 MLP 的隐藏层学习到 “(\Phi(x) \times \Phi(x))” 的非线性交互。

例子：文档第五部分的彩色 MNIST 实验：

• 真实不变性是非线性的：“数字形状特征（(\Phi(x))）与标签Y的关系” 需要非线性映射（如 “像素组合→形状特征→概率”）；
• 用 MLP（非线性分类器）作为(\Phi)，既能捕捉 “形状特征”，又能通过非线性激活函数学习 “形状→标签” 的非线性不变性，最终在测试环境中泛化成功。

3. IRM 中的选择：为什么用非线性分类器（(\Phi)）+ 固定线性w？

文档第三部分的 IRMv1 用 “非线性(\Phi)（如神经网络）+ 固定线性(w=1.0)”，本质是 “让(\Phi)承担‘非线性特征提取’的任务，让w承担‘线性传递’的任务”—— 这种设计的巧妙之处在于：

• 非线性(\Phi)负责 “从原始输入中提取不变特征（无论线性还是非线性）”：比如(\Phi)可以提取 “(x^2)”（非线性不变特征），也可以提取 “x”（线性不变特征）；
• 固定线性(w=1.0)负责 “传递不变特征到输出”：无需优化w，只需让(\Phi)输出 “已处理好的不变特征”，(w=1.0)直接传递，避免参数冗余和作弊。

这种设计既利用了非线性分类器的灵活性（捕捉非线性不变性），又通过固定w简化了优化（避免缩放作弊）—— 是 “灵活性” 与 “可优化性” 的平衡。

四、常见误区澄清

1. **误区 1：线性分类器只能学习线性不变性，非线性分类器只能学习非线性不变性？**错。非线性分类器可以学习线性不变性（只需关闭非线性激活），但线性分类器无法学习非线性不变性 —— 核心是 “分类器的表达能力是否覆盖不变性的函数形式”。
2. **误区 2：IRMv1 的(w=1.0)是线性的，所以 IRM 只能学习线性不变性？**错。IRMv1 的w是线性的，但(\Phi)可以是非线性的 ——(\Phi)可以提取 “非线性的不变特征”（如(\Phi(x) = x^2)），此时(w \cdot \Phi(x) = x^2)，本质是学习了 “(Y = x^2)” 的非线性不变性。w的线性与否，不影响(\Phi)的非线性特征提取能力。
3. **误区 3：非线性不变性一定比线性不变性更好？**错。不变性的 “线性 / 非线性” 是 “真实规律的属性”，不是 “优劣的判断标准”—— 如果真实规律是线性的（如示例 1 的(Y = X_1)），用非线性分类器反而可能过度拟合（学习到 “(X_1 + X_1^3)” 等冗余项），降低泛化能力。

总结：四者关系的核心逻辑

概念	核心描述	IRM 中的作用
线性分类器	输入特征的一次函数，决策边界线性	仅用于简单线性不变性场景（如示例 1），表达能力有限
非线性分类器	输入特征的非线性函数，决策边界复杂	核心工具（如(\Phi)用 MLP/CNN），捕捉线性 / 非线性不变性
线性不变性	不变特征与Y的线性稳定关联	简单因果规律的体现（如物理定律、线性回归）
非线性不变性	不变特征与Y的非线性稳定关联	复杂现实规律的体现（如图像分类、复杂物理过程）

简单说：分类器是 “工具”，不变性是 “目标”—— 选择线性还是非线性分类器，取决于 “真实不变性的函数形式”；而 IRM 的价值在于，无论不变性是线性还是非线性，都能通过 “灵活的(\Phi) + 固定的w”，学习到跨环境稳定的关联，实现分布外泛化。

6. 特征分布不一定是因果关联

一、先明确：因果关联与特征分布的核心区别

在 “白天（e1）/ 夜晚（e2）猫分类” 任务中：

• 因果关联：指 “猫的真实特征（如轮廓）→标签 Y” 的稳定关系，即(P(Y|X_{轮廓})^e1 = P(Y|X_{轮廓})^e2)—— 无论白天还是夜晚，“有猫的轮廓→Y = 猫” 的概率始终是 90%，这是我们需要保留的核心；
• 特征分布：指 “输入特征 X（或表示 Φ(X)）的边际分布”，即(P(X)^e1)（白天猫的像素分布：明亮、细节清晰）和(P(X)^e2)（夜晚猫的像素分布：昏暗、细节模糊）—— 两者天然不同，是环境差异的体现。

“匹配特征分布” 的思路（如领域自适应）试图让(P(Φ(X))^e1 = P(Φ(X))^e2)（比如把夜晚猫的 Φ(X)“提亮”，让其分布和白天一致），但这种操作会强行抹除 “环境差异中与因果关联无关的合理信息”，甚至扭曲因果特征本身。

二、具体场景：匹配特征分布如何破坏因果关联

以 “白天 / 夜晚猫” 为例，假设 Φ(X) 是 “提取猫轮廓的特征表示”，我们分两步看 “匹配分布” 的危害：

1. 第一步：为匹配分布，Φ 被迫 “篡改因果特征”

白天猫的轮廓特征 Φ(X1)：边缘清晰（如耳朵轮廓的梯度值大）、像素强度高（均值 200）；夜晚猫的轮廓特征 Φ(X2)：边缘模糊（梯度值小）、像素强度低（均值 50）；两者的边际分布(P(Φ(X)))天然不同（均值、方差都不一样）。

若强行要求(P(Φ(X))^e1 = P(Φ(X))^e2)，模型会怎么做？

• 要么 “把夜晚猫的 Φ(X2) 强度拉高到 200”：但夜晚猫的真实轮廓是模糊的，拉高强度会导致 “非轮廓区域（如背景噪声）也被强化”—— 原本 “模糊轮廓→Y = 猫” 的因果关联被破坏，模型可能把 “噪声强化的背景” 误判为猫；
• 要么 “把白天猫的 Φ(X1) 强度压低到 50”：白天猫的清晰轮廓被模糊，原本 “清晰轮廓→Y = 猫” 的高概率（90%）会下降到 “模糊轮廓→Y = 猫” 的低概率（60%）—— 因果关联的强度被削弱，模型无法再依赖轮廓做准确判断。

简言之：因果特征的分布差异（白天清晰 / 夜晚模糊）是 “环境差异的自然结果”，强行匹配会让 Φ(X) 偏离 “真实因果特征”，导致因果关联断裂。

2. 第二步：匹配分布可能 “引入虚假关联”，进一步掩盖因果

假设 “白天猫的背景多为白色，夜晚猫的背景多为黑色”—— 背景颜色是 “非因果特征”（与 Y 无关），但为了匹配 Φ(X) 的分布，模型可能会：

• 把夜晚猫的背景 “从黑色改成白色”，让 Φ(X) 的颜色分布和白天一致；
• 此时，Φ(X) 中 “背景颜色” 的权重被放大，而 “轮廓” 的权重被压缩（因为轮廓的分布差异已被强行抹除）。

最终结果：模型会误以为 “白色背景→Y = 猫”（虚假关联），而忽略 “轮廓→Y = 猫” 的因果关联 —— 这和 ERM 依赖 “绿色背景 = 奶牛” 的错误逻辑完全一致，本质是 “为了匹配分布，牺牲了因果特征的优先级”。

三、数学层面：为什么 “P (Φ(X)) 一致”≠“P (Y|Φ(X)) 一致”

“匹配特征分布” 的核心误区是：认为 “P (Φ(X)) 一致” 能推出 “P (Y|Φ(X)) 一致”（因果关联稳定），但数学上两者没有必然联系，甚至可能冲突。

用贝叶斯公式拆解：(P(Y|Φ(X)) = \frac{P(Φ(X)|Y) \cdot P(Y)}{P(Φ(X))})

“匹配特征分布” 仅保证(P(Φ(X))^e1 = P(Φ(X))^e2)，但：

1. (P(Y))（标签分布）可能随环境变（如白天猫样本占 80%，夜晚占 20%）—— 此时即便(P(Φ(X)|Y))和(P(Φ(X)))一致，(P(Y|Φ(X)))也会变；
2. 更关键的是：为了让(P(Φ(X)))一致，模型可能扭曲(P(Φ(X)|Y))（“因果特征→Y” 的条件分布）—— 比如把 “夜晚猫的 Φ(X|Y = 猫)” 改成和 “白天猫的 Φ(X|Y = 猫)” 一致，导致(P(Y|Φ(X)))失去因果意义。

举个极端例子：若 Φ(X) 被强制 “所有环境下都输出同一个值”（完全匹配分布），则(P(Y|Φ(X)) = P(Y))（仅依赖标签分布），因果关联被完全破坏 —— 模型变成 “靠猜标签分布分类”，和因果无关。

四、附录 D 的核心观点：匹配分布是 “为了不变而不变”，偏离因果目标

附录 D（IRM 实现细节的补充）明确指出：“试图让 Φ(X) 的支撑集（或分布）一致” 的思路，本质是 “追求表面的不变性（特征分布不变），而非本质的不变性（因果关联不变）”。

这种思路的根本问题在于：

• 因果关联的稳定，不依赖 “特征分布的稳定”—— 比如 “猫的轮廓→Y = 猫” 的关联，无论轮廓特征是清晰还是模糊（分布不同），只要 “轮廓存在”，关联就稳定；
• 强行匹配分布，会让 Φ 失去 “捕捉因果特征的灵活性”——Φ 的目标应该是 “提取‘无论分布如何变，都能稳定预测 Y’的因果特征”，而不是 “把所有环境的特征都改成同一个分布”。

总结：为什么 IRM 不采用 “匹配特征分布”

IRM 的核心是 “追求 P (Y|Φ(X)) 跨环境不变”（因果关联稳定），而 “匹配特征分布” 追求的是 “P (Φ(X)) 跨环境不变”（表面分布一致）—— 前者是 “因”，后者是 “果”：

• 若因果关联稳定（P (Y|Φ(X)) 不变），即便 P (Φ(X)) 变，模型也能泛化；
• 若强行让 P (Φ(X)) 不变，反而可能破坏因果关联，导致泛化失败。

这就是 “匹配特征分布会破坏因果关联” 的本质 —— 它颠倒了 “不变性” 的优先级，把 “环境差异的表面特征” 当成了 “不变性的目标”，最终偏离了 “捕捉因果关联” 的核心。

7. 容量最小的零误差解

• 零误差解：在一些计算或模型拟合任务中，零误差解指的是能够完全准确地满足给定条件或数据的解，即不存在任何误差。例如，在解方程时，如果某个解使得方程左右两边完全相等，没有任何偏差，那么这个解就是零误差解。在机器学习中，如果一个模型能够完美地拟合训练数据，对于每个训练样本都能准确预测其输出，那么该模型对应的参数设置就是一个零误差解。
• 容量最小：“容量” 在这里通常可以理解为模型的复杂度或表示能力。容量最小的模型意味着它具有最简单的结构或最少的参数数量。例如，在神经网络中，层数较少、神经元数量较少的网络相对来说容量较小。追求容量最小的零误差解，就是在能够找到满足零误差条件的解的前提下，选择其中模型容量最小的那个解。

综合起来，“容量最小的零误差解” 就是在所有能够精确满足给定条件或数据（即零误差）的解中，具有最小模型复杂度或表示能力的解。这种解在实际应用中具有重要意义，因为它通常具有更好的泛化能力，不容易出现过拟合现象，能够在新的数据上也有较好的表现。